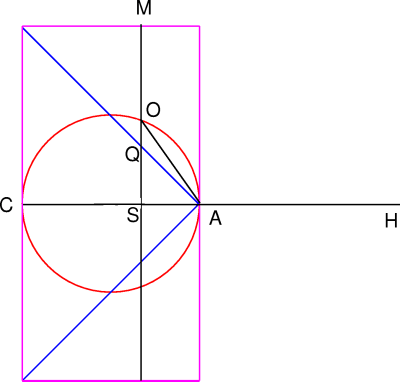


The areas of the three discs in question are proportional to the square of their radii. With points labeled as in this diagram (adapted from T. L. Heath, The Works of Archimedes with The Method of Archimedes, Dover, New York), the equation m d = M D from the previous page becomes
MS2.SA = (OS2 + QS2).AH .
Since AH = CA it follows that
AH/SA = CA/SA = MS/SQ (substituting
equals for equals) = MS2/MS.SQ = MS2/(OS2 + SQ2). Cross-multipling gives the desired equation.
4. The plane geometry behind the argument