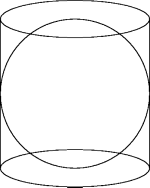
Vol(Sphere) + Vol(Cone) = (1/2)Vol(Large Cylinder).


|
Archimedes determined the ratio of the volume of a
sphere to the volume of the circumscribed cylinder. The actual
construction involves the cylinder concentric to the circumscribed
cylinder but with double the diameter (and consequently four
times the volume). Another essential ingredient
is the cone with the same base as the large cylinder, and with
the same height. According to Euclid, XII, 10 (this link is to the invaluable
Perseus Project at Tufts)
the volume of that cone is 1/3 the volume of the cylinder. What
Archimedes gets from his Method is the equation:
Vol(Sphere) + Vol(Cone) = (1/2)Vol(Large Cylinder). |
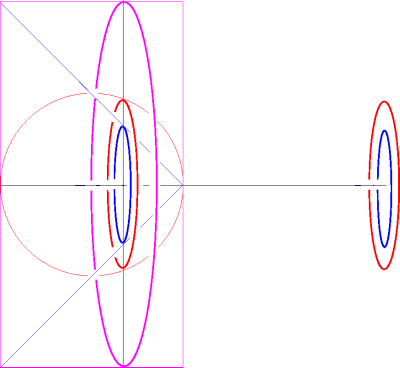
The balancing argument runs as follows. We imagine the sphere (red) the cone (blue) and the large cylinder (mauve) to be set up horizontally, as shown here,
| 
|
If we imagine doing this for all the slices together, we will have balanced, on the right, the entire sphere and the entire cone, their masses concentrated at the end-point of the axis, and on the left the cylinder in its original position, since none of its slices had to be moved. The balancing force of the cylinder is the same if all of its mass is concentrated at its center of mass, which is halfway down the axis to the left. The equation for balancing masses m and M at distances d and D on opposite sides of the fulcrum is m d = M D. Here m is the mass of the cylinder, d is half the height of the cylinder, M is the sum of the masses of sphere and cone, and D is the height of the cylinder. It follows that M = (1/2)m, the equation we needed.