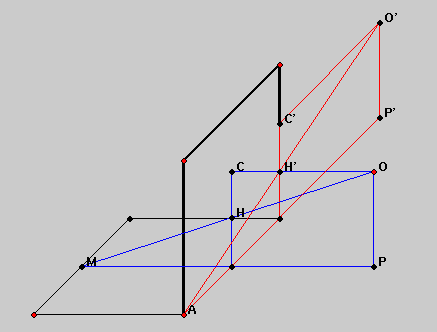


The checkerboard is horizontal and abuts the edge of the (vertical) frame. A point O' is drawn in the picture-plane (to the right in this illustration), on a level with the vanishing-point C, and such that the horizontal distance O'C' to the frame is equal to the distance OC from the eye to C. Let M be the point where the far edge of the checkerboard intersects the vertical plane through O and C. The line of sight OM cuts the picture plane at H. To construct the image of the far edge of the checkerboard, it is enough to know the height of H. Since the checkerboard is square, the figure O'C'H'AP' is congruent to the figure OCHMP: the height of H is the same as the height of H' which is the intersection of O'A with the right-hand edge of the frame.
In this way the three-dimensional (blue) construction collapses into the 2-dimensional (red) one, and the perspective problem admits an elementary geometric solution.
|
|
|
© Copyright 2001, American Mathematical Society |