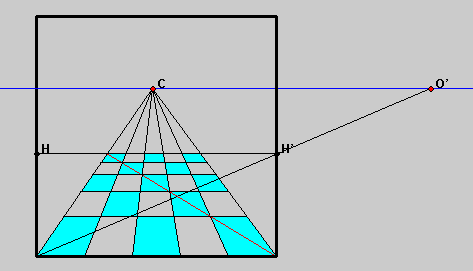
| Alberti's pavement construction. The eye is across from point C, looking through the vertical frame at a horizontal checkerboard abutting the lower edge of the frame. To realize on the picture what the eye sees, locate the point O' on the (blue) horizon (the horizontal through C) at a distance from the edge of the frame equal to the distance from the eye to C. If the construction is done, as here, to the right, join O' to the left-land lower corner of the frame. The horizontal HH'through the intersection of this line with the right-hand edge of the frame gives the farther edge of the image of the checkerboard. The lines separating the columns of the checkerboard come from joining to the vanishing point the corresponding points on the lower edge of the frame. The location of the lines separating the rows is given by the intersections of the (red) diagonal with that fan of lines. Click on figure for JAVA-animation. |
