MAT 320 Introduction to Analysis
Fall, 1996
NOTE (11/15/96): See Revised Syllabus; Optional
Second Midterm.
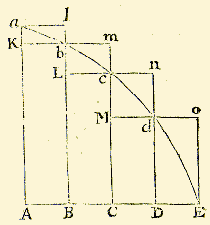This figure from Isaac Newton's
Principia Mathematica (1686) illustrates his Lemma II
which states, in modern terminology, that for a
monotonic function the left- and right-hand sums have
the same limit, which is the area under the curve.
I have edited out some lines and notation referring
to a different lemma.
Press here to see
the full Latin text of Lemma and Proof, with a
translation into English. Press
here for an animated version of Newton's diagram, due to
Stony Brook student Vladimir Livshits. Clicking on the difference
rectangles makes them slide into a single column.
Meets Tu-Th 10-11:20 in Harriman 104.
Text: Michael C. Reed, Fundamental Ideas of Analysis
Pre-publication version; Wiley.
This edition of the book is being distributed to us
for free. In return, please mark carefully in your copy
any misprints or errors you find, as well as any passages you find
hard to understand, and please turn in your books at the
end of the term (you can have them back eventually).
Wiley is giving us some money we can use for a pizza party at
the end of classes.
Roster
Staff
Syllabus
Homework
Week by week
Review for Midterm 1
Midterm 1
Review for Midterm 2
Midterm 2 (track B)
Review for Final
Final Exam (track A)
Final Exam (track B)
Here is a link
to an Interactive Real Analysis
page under development at Seton Hall University.
(``Interactive Real Analysis is an online, interactive textbook
for Real Analysis or
Advanced Calculus in one real variable. It deals with sets, sequences, series,
continuity, differentiability, integrability (Riemann and Lebesgue),
topology, and more.'')
Grading Policy
Homework 20%
Midterm 30%
Final 50%
Homework will be collected each Thursday.
I have two main goals in this course. First to acquaint you
with the mathematical foundations of the Calculus and at the
same time to introduce you to some of the many mathematical
phenomena related to the Calculus. Second is to train you
in the construction and analysis of mathematical proofs.
I will try to assign each week at least one homework exercise that
involves making up a proof.
Format for Proofs. Please follow the following format in
submitting proofs. This will allow you to assemble them into a
portfolio at the end of the semester.
- Each proof should be on a page or pages by itself. Put
name, course number and date due at the top of the page.
- Begin with words of introduction (only if
necessary). For example the Catalan number exercise could
start with "The Catalan numbers are defined by C(1)=1,
C(2)=2 and the recursion relation ......"
The statement to be proved should be
prefaced by the words "Theorem," "Proposition," etc.,
whatever you feel is appropriate.
- The proof should begin with: "Proof." and end
with "QED" or "which completes the proof" (if
appropriate) or some such words to show that the argument is over.
- The text of the proof must be in clear, correct,
grammatical English. I will instruct the grader to
return for correction all homework that does not
meet this requirement.
- The argument must be presented in enough detail so
that you could give it to one of your classmates to read.
- Last but not least, the argument must be
complete and mathematically correct!!
Disabilities. If you have a physical, psychological, medical
or learning disability that may impact on your ability
to carry out assigned course work, I would urge that you
contact the staff in the Disabled Student Services office
(DSS), Room 133 Humanities, 632-6748/TDD. DSS will review
your concerns and determine, with you, what accommodations
are necessary and appropriate. All information and
documentation of disability is confidential.