MAT 320 Introduction to Analysis
December 19, 1996 Final Examination
A-track
THIS TEST IS ``OPEN BOOK.'' TOTAL SCORE = 100.
1. (10 points)
Prove that the function 
is continuous, but not uniformly continuous, on the open
interval (0,1).2. (10 points)
Consider a continuous function f defined on [0,1] and
with values in [0,1], i.e. such that 
for every x in [0,1]. Show that f has a fixed point,
i.e. that there is a point x in [0,1] such that f(x)=x.
Hint: Consider the function g(x)=f(x)-x.
3. (10 points) Consider the function
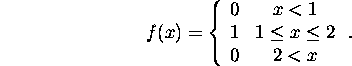
Prove carefully and directly that f is Riemann integrable on [0,3]. ``Directly'' means show that f satisfies the definition of Riemann integrability; DO NOT use Theorem 3.5.2!
4. (20 points) Consider the function
a. Show that this function is differentiable at x=0.
b. Show that f is continuously differentiable, i.e. that f' is a continuous function.
5. (30 points)
Consider the problem of calculating 
by applying Newton's method to find a root of 
.
Show that if
is any number greater than , then the
numbers 
calculated by iterating Newton's
method give a sequence converging to . Proceed as
follows.
NOTE: the various parts of this problem may be worked
independently: assume that earlier parts are proven.
a. Show that if 
then
(Hint: for the first inequality, draw the graph of f and argue using its convexity.)
b. Conclude that the sequence 
has a limit
as 
.
c. Show that the limit must be .
d. What happens if the initial guess lies
strictly between 0 and ?
6. (10 points) Suppose 
is a sequence of
bounded functions which converges uniformly to a limit function f.
Prove that f is bounded.
7. (10 points)
Suppose the function f is (n+1) times continuously
differentiable on [0,1], and that its (n+1)-st derivative
is bounded in absolute value by M.
Prove that
can be approximated by
with an error less than 
in absolute
value.