This is an 80-minute test. Work all questions.

1. (20 points) Let f be a continuous function defined on the closed interval [a,b]. Prove that |f| is bounded, i.e. that there exists a number M such that for all .

2. (20 points). The function is monotonic increasing on . Find n so that a left-hand sum with n equal subdivisions is within .01 of .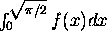

3. (20 points) Prove that

is differentiable at x=0. What is the value of its derivative there?

4. (20 points) Prove that

is a convergent integral, i.e. that the integrals from 1 to c tend to a finite limit L as .

5. (20 points) Suppose f is continuously differentiable, and that for all x. If f(1)=1, how large can f(2) possibly be?

• About this document ...