


Next: Pseudo-random number generators
Up: Probabilistic Encryption
Previous: Semantic Security
Contents
Subsections
We will not analyze an entire game of poker, but just the task
of each player [we will assume only two players]
getting dealt cards so that (i) each player gets his cards at
random, with all cards equally likely (ii) neither player knows
what his opponent has (iii) the players cannot get the same cards.
You will probably appreciate the procedure more if you first try
to devise a way of doing this yourself.
Several previous attempts to use cryptographic devices for this
purpose were flawed12.
The elaborate procedure we describe is based on some number-theory
tools developed in section 3.3
and earlier in this section:
- If
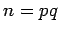 and
and  is a square mod
is a square mod 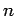 , it has four square
roots. If we know roots
, it has four square
roots. If we know roots 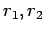 with
with
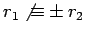 ,
we can find
,
we can find  ,
, 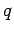 .
.
- If
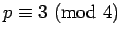 ,
,  is a square mod
is a square mod  if and only if
if and only if 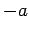 is not a square (Lemma 22).
If we also have
is not a square (Lemma 22).
If we also have
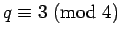 ,
then
,
then 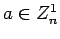 if and only if
if and only if 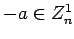 .
.
- We can test whether
or not
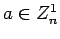 without knowing
without knowing 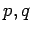 .
.
Two techniques are used repeatedly. They are also of interest
in other applications.
Theorem 27 (random numbers)
B can generate
a random number so that A does not know its value now, but can
verify it later.
A ``first try'' might be for B to generate
a random number and give an encryption of it to A, with the key
revealed for verification later. This does not work, since
A cannot be sure that B chose his number at random.
To insure
randomness, A gives B a second number (which A is supposed to
choose at random) after receiving B's encryption,
and the number used by B is the ``exclusive or'' of the two:
| A chooses 0110001 |
| B chooses 1011011 |
| B uses 1101010 |
Even if one of the players does not choose his number at random,
the result will be random as long as the other player does.
Theorem 28
B can ask A a question related to 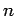 . The answer to
this question may or may not allow B to factor
. The answer to
this question may or may not allow B to factor 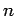 . At the time
the question is asked, A cannot tell whether the answer he gives
B is useful or useless, but this can be verified later.
. At the time
the question is asked, A cannot tell whether the answer he gives
B is useful or useless, but this can be verified later.
Proof: A chooses primes
 , and announces
, and announces 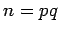 .
Using the technique of Theorem 27, B generates a random
.
Using the technique of Theorem 27, B generates a random  , and
will ask A for a square root of
, and
will ask A for a square root of 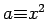 . At the time the
question is asked, A will know
. At the time the
question is asked, A will know  but not
but not  . B is allowed to
specify whether the square root A gives him is or is not in
. B is allowed to
specify whether the square root A gives him is or is not in 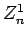 .
.
If 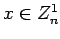 and B specifies that the square root is in
and B specifies that the square root is in 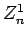 ,
A will give B
,
A will give B 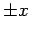 , which is useless. B can get useful information
by specifying that the square root is not in
, which is useless. B can get useful information
by specifying that the square root is not in 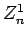 . If
. If
 ,
the square root in
,
the square root in 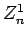 will be useful, and the other will be
useless.
will be useful, and the other will be
useless.
Since  is randomly chosen, and half the possible
is randomly chosen, and half the possible
 are in
are in 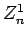 and half are not, A will not be able to guess
right more than half the time whether he is being asked for useful
or useless information.
and half are not, A will not be able to guess
right more than half the time whether he is being asked for useful
or useless information.
- A announces
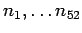 , each of
which is a product of two large primes
, each of
which is a product of two large primes
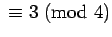 . He encodes the
names of the different cards using different
. He encodes the
names of the different cards using different 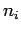 and also announces
these. [if B finds the factors
of one of the
and also announces
these. [if B finds the factors
of one of the 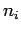 , it does not help him identify the other cards]
B does the same thing using
, it does not help him identify the other cards]
B does the same thing using
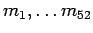 .
.
- To get a card, B asks A one question for each
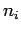 , using
the procedure of Theorem 28. 51 of the questions will be useless.
The useful question allows B to decode the name of the card he
receives. [it is crucial that A will be able to verify the uselessness
of the other 51 questions after the game.]
, using
the procedure of Theorem 28. 51 of the questions will be useless.
The useful question allows B to decode the name of the card he
receives. [it is crucial that A will be able to verify the uselessness
of the other 51 questions after the game.]
- B deletes the
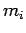 corresponding to the card he received
(this ensures A will not get this card).
corresponding to the card he received
(this ensures A will not get this card).
- A gets a card by asking 51 questions about the remaining
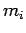 , of which 50 are useless.
He deletes the
, of which 50 are useless.
He deletes the 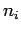 corresponding to this card.
corresponding to this card.
- If B gets a second card, he asks 51 questions. He avoids
getting the same card twice by not asking a useful question about
the same
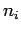 as the first time.
as the first time.
This procedure is too cumbersome to be practical, but it is a good
example of the kinds of things that can be done using cryptographic
procedures. Current research focusses on other tasks involving
exchanges of encrypted and partially encrypted information between
two players.
Footnotes
- ... flawed12
- R. Lipton, ``How to cheat at mental
poker,'' Proceedings of AMS Short Course on Cryptography



Next: Pseudo-random number generators
Up: Probabilistic Encryption
Previous: Semantic Security
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() and B specifies that the square root is in
and B specifies that the square root is in ![]() ,
A will give B
,
A will give B ![]() , which is useless. B can get useful information
by specifying that the square root is not in
, which is useless. B can get useful information
by specifying that the square root is not in ![]() . If
. If
![]() ,
the square root in
,
the square root in ![]() will be useful, and the other will be
useless.
will be useful, and the other will be
useless.
![]() is randomly chosen, and half the possible
is randomly chosen, and half the possible
![]() are in
are in ![]() and half are not, A will not be able to guess
right more than half the time whether he is being asked for useful
or useless information.
and half are not, A will not be able to guess
right more than half the time whether he is being asked for useful
or useless information.