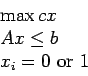Next: Terminology
Up: Subset-Sum Problems and NP-Completeness
Previous: Converting (SSP) to (SP)
Contents
It is more important to understand the
general idea of what we did in section 5.3 than to get involved in
the details of the construction of the ``adding machine.'' We used
logical variables (the  ) to represent our guess as to what a solution
to the (SSP) was, then constructed a set of formulas to verify the
guess was correct.
) to represent our guess as to what a solution
to the (SSP) was, then constructed a set of formulas to verify the
guess was correct.
You should be able to convince yourself that a
similar thing could be done with a factoring problem. We could have
variables  and
and 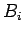 represent our guesses as to two factors, then
construct a ``multiplication machine'' to verify that the product is
what we want. Thus an efficient algorithm for (SP) would lead to an
efficient algorithm for factoring6.
represent our guesses as to two factors, then
construct a ``multiplication machine'' to verify that the product is
what we want. Thus an efficient algorithm for (SP) would lead to an
efficient algorithm for factoring6.
Many other problems can be viewed as making some guesses
as to what the correct answer is, with the process of verification
relatively easy. An example might be an integer programming problem:
We ask if there is a feasible solution with objective function value 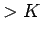 .
For a given
.
For a given 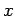 , it is easy to check that it satisfies all the problem
constraints and tell if the value is big enough.
, it is easy to check that it satisfies all the problem
constraints and tell if the value is big enough.
The detailed
construction in section 5.3 was intended primarily to convince
you that, if a verification can be done efficiently, it can be
simulated by a set of logic formulas. It should make you willing to
believe
Theorem 18 (Cook)
Any ``guess and verify'' problem can be converted
to a satisfiability problem. Thus, an efficient algorithm for (SP) can
efficiently solve any ``guess and verify'' problem.
Footnotes
- ... factoring6
- Unlike (SSP), nobody has
been able to show that an algorithm for factoring would give an algorithm
for (SP).




Next: Terminology
Up: Subset-Sum Problems and NP-Completeness
Previous: Converting (SSP) to (SP)
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() and
and ![]() represent our guesses as to two factors, then
construct a ``multiplication machine'' to verify that the product is
what we want. Thus an efficient algorithm for (SP) would lead to an
efficient algorithm for factoring6.
represent our guesses as to two factors, then
construct a ``multiplication machine'' to verify that the product is
what we want. Thus an efficient algorithm for (SP) would lead to an
efficient algorithm for factoring6.