We will represent numbers in base 2. Since all relevant numbers are
![]() , numbers may be represented by 26 logical variables. For each
, numbers may be represented by 26 logical variables. For each
![]() , we will have variables
, we will have variables
![]() .
These will represent
.
These will represent
![]() if
if ![]() , 0 if
, 0 if ![]() . To do this, we need formulas which show
how the value of
. To do this, we need formulas which show
how the value of ![]() determines the value of all the
determines the value of all the ![]() :
:
Next, we need, for ![]() , variables
, variables
![]() which represent the total of the first
which represent the total of the first ![]() of the numbers given by the
of the numbers given by the
![]() -variables. Formulas are needed which show the
-variables. Formulas are needed which show the ![]() -variables determining the
-variables determining the ![]() -variables.
-variables.
We begin with a set of formulas
![]() which have
which have ![]() get value T if and only if an odd number
of
get value T if and only if an odd number
of ![]() have value T.
have value T. ![]() gets value T if and only if
2 or 3 of
gets value T if and only if
2 or 3 of ![]() have value T:
have value T:
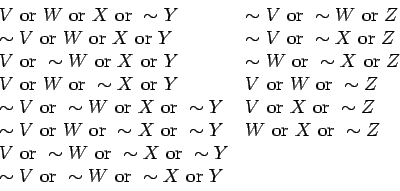
We will use ![]() ,...,
,...,![]() ,
, ![]() , to keep track of
numbers being carried. Since there are no numbers carried in the rightmost
column, we have the formulas
, to keep track of
numbers being carried. Since there are no numbers carried in the rightmost
column, we have the formulas ![]() . The formulas
. The formulas
These logic formulas together have the effect that the ![]() determine the
determine the ![]() ,
which determine
,
which determine ![]() through
through ![]() successively. This last group
of variables corresponds to the base-2 representation of the sum of
the
successively. This last group
of variables corresponds to the base-2 representation of the sum of
the ![]() which are in the set we have chosen. Finally, we add the formulas
which are in the set we have chosen. Finally, we add the formulas
![]() or
or ![]() depending on whether the
depending on whether the ![]() th
digit of
th
digit of ![]() is 1 or 0. As planned, a solution to this satisfiability
problem gives a solution to the subset-sum problem (look at which
is 1 or 0. As planned, a solution to this satisfiability
problem gives a solution to the subset-sum problem (look at which ![]() have value T), which implies that a method of solving (SP) can be used
to solve (SSP).
have value T), which implies that a method of solving (SP) can be used
to solve (SSP).
The (SP) we have constructed is rather large,
involving approximately ![]() formulas. However, the rate of
growth if we had more
formulas. However, the rate of
growth if we had more ![]() with a larger upper limit is not too bad.
with a larger upper limit is not too bad.