Next: The int (and Int) Up: Preliminaries about Maple Previous: The limit command

Subsections

Higher order derivatives
Implicit differentiation

The diff (and Diff) command

The diff command is used to compute derivatives of Maple expressions. Its syntax is basically

> 
  diff(f,x);

where f is an algebraic expression and x is the variable with respect to which the derivative is taken. For example, to compute

$\displaystyle {\frac{d}{dx}}$ $\displaystyle {\frac{3x-6}{x^2-4}}$ ,

we execute the Maple command

> 
  diff((3*x-6)/(x^2-4),x);

$\begin{maplelatex} \begin{displaymath} \frac{3}{x^2 -4} - 2 \frac{(3x -6)x}{\left(x^2 -4\right)^2} \end{displaymath}\end{maplelatex}$

You must specify the variable with respect to which you wish to take the derivative because, almost all the time, there are constants and other parameters around:

> 
  diff(exp(a*x),x);

$\begin{maplelatex} \begin{displaymath} a e^{a x} \end{displaymath}\end{maplelatex}$

Maple knows theoretical results about derivatives. For example, even if the functions g(x) and h(x) are not defined, Maple will give you the derivative of their product in terms of the functions and their derivatives:

> 
  diff(h(x)*g(x),x);

$\begin{maplelatex} \begin{displaymath} \left( \frac{\partial}{\partial x} h(x) \... ...eft( \frac{\partial}{\partial x} g(x) \right) \end{displaymath}\end{maplelatex}$

Higher order derivatives

To compute higher order derivatives, you can of course iterate the above command:

> 
  diff(diff(3*sin(x),x),x);

$\begin{maplelatex} \begin{displaymath} - 3 \sin(x) \end{displaymath}\end{maplelatex}$
Such a command first calculates the derivative with respect to x of the expression 3*sin(x) and then differentiates the result to obtain the second derivative. The same result can be accomplished with either one of the following commands:

> 
  diff(3*sin(x),x,x);

$\begin{maplelatex} \begin{displaymath} - 3 \sin(x) \end{displaymath}\end{maplelatex}$

> 
  diff(3*sin(x),x
2);

$\mapleresult$ $\begin{maplelatex} \begin{displaymath} - 3 \sin(x) \end{displaymath}\end{maplelatex}$

Thereisanobviousextensionofthiscommandwhencalculatingmorethantwoderivatives.Youcanalsocalculatepartialderivativesofhigherorder : $\MI$

diff (ln(x)*exp(- 2*x), x3);
$\begin{maplelatex} \begin{displaymath} 2\frac{e^{-2x}}{x^3} + 6\frac{e^{-2x}}{x^2} + 12\frac{e^{-2x}}{x} - 8\ln(x) e^{-2x} \end{displaymath}\end{maplelatex}$

> 
  diff(exp(x)*y^2*sin(z),x,y,z);

$\begin{maplelatex} \begin{displaymath} 2 e^x y \cos(z) \end{displaymath}\end{maplelatex}$

Implicit differentiation

Maple knows how to take derivative of both sides of an equation, and, as indicated above, Maple can also take derivatives ``theoretically'' even if the definition of the functions involved are not specified. However, you must always indicate explicitly the dependence of the functions on their variables. So, if you are thinking of y as a function of x, you must write y(x) in your equation rather than just y.

Here is a typical implicit differentiation problem. Consider the equation x²y - 3y³x = 0. Find the slope of the graph of the curve defined by this equation at the point (3, 1):

> 
  eq:=x^2*y(x)-3*y(x)^3*x = 0; 
  deq:=diff(eq,x);
  solve(deq,diff(y(x),x));

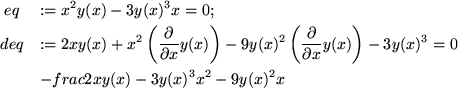
$\begin{maplelatex} \begin{eqnarray*} & eq & := x^2 y(x)-3y(x)^3 x = 0; \\ & deq... ...& & -frac{2 x y(x) - 3 y(x)^3}{x^2 - 9 y(x)^2 x} \end{eqnarray*}\end{maplelatex}$

> 
  subs(y(x)=1,x=3,

$\begin{maplelatex} \begin{displaymath}\frac{1}{6} \end{displaymath}\end{maplelatex}$

The first command defines the equation relating x and y, the second defines an equation deq giving the relation between x, y(x) and the derivative of y with respect to x. Using solve, we solve deq to find the derivative as a function of x and y(x), and in the result we substitute x=3 and y=1 to obtain the desired slope (see section 8 to learn about the subs command).^1.12

Maple actually has a built-in command to do implicit differentiation, implicitdiff. Thus, we could have done this same problem more concisely using the single command

> 
  subs(y=1,x=3,  implicitdiff(x^2y-3y^3x=0,y,x);

$\begin{maplelatex} \begin{displaymath}\frac{1}{6} \end{displaymath}\end{maplelatex}$

Occasionally, to make your worksheets easier to read, you may wish to have Maple display a derivative in standard mathematical notation without evaluating it. For this purpose there is an inert capitalized form of the diff command: Diff. The two forms diff and Diff are usually combined to produce meaningful sentences:

> 
  Diff(exp(x)/(1-x),x);

$\begin{maplelatex} \begin{displaymath}\frac{\partial}{\partial x}\frac{e^x}{1-x} \end{displaymath}\end{maplelatex}$

> 
  Diff(exp(x)/(1-x),x)=diff(exp(x)/(1-x),x);

$\begin{maplelatex} \begin{displaymath}\frac{\partial}{\partial x}\frac{e^x}{1-x}=\frac{e^{x}}{1-x}+ \frac{e^{x}}{(1-x)^2} \end{displaymath}\end{maplelatex}$

This command is particularly useful to produce easy to read worksheets that involve partial derivatives:

> 
  f:=x^3*exp(y)-sin(x*y);

$\begin{maplelatex} \begin{displaymath}f:= x^3 e^y - \sin(x y) \end{displaymath}\end{maplelatex}$

> 
  Diff(f,x,x,y)=diff(f,x,x,y);

$\begin{maplelatex} \begin{displaymath}\frac{\partial ^3}{\partial y \partial x^2... ...n{(xy)} = 6 x e^y+\cos{(xy)}xy^2+2\sin{(xy)}y \end{displaymath}\end{maplelatex}$

Footnotes

... command).^1.12: Again, the major caveat with the Maple derivative command is to avoid calculating derivatives with respect to a variable that has been previously given a value. In such an instance, unassign the value of the variable first.

Next: The int (and Int) Up: Preliminaries about Maple Previous: The limit command

Translated from LaTeX by Scott Sutherland
2002-08-29