The limit command

The limit command is used to compute limits. Its syntax is basically

> 
  limit(f,x=a);

where f is a Maple algebraic expression which (in general) depends on the variable x and a is the expression which x approaches. For example, to compute

$$\lim_{x\rightarrow 2}^{}$$$${\frac{3x-6}{x^2-4}}$$ ,

we execute the Maple command

> 
  limit((3*x-6)/(x^2-4),x=2);

Maple can also deal with limits which do not exist, for example $$\lim_{x\rightarrow 0}^{}$$$${\frac{1}{x}}$$:

> 
  limit(1/x,x=0);

In the following exercise, we define the slope of a straight line passing through the points (x₁, y₁), (x₂, y₂), use this function to find the slope m(x) of the line passing through the points (1, 1) and (x, x²), and finally compute the limit of m(x) as x $\rightarrow$ 1:

> 
  slope:=(x1,y1,x2,y2)->(y2-y1)/(x2-x1);
  m:=x->slope(1,1,x,x^2);

> 
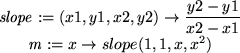
  limit(m(x),x=1);

Maple is sometimes unable to determine a limit or whether it exists. In such a case, it will return nothing after you execute the limit command.

Maple computes two-sided limits. For example, if you specify the argument x=1 as in the previous example, Maple assumes you mean that x approaches 1 from either the right or the left through real values only (as opposed to complex ones). However, Maple can compute one sided and complex limits also:

> 
  limit(1/x,x=0,right);

> 
  limit(1/x,x=0,left);

> 
  limit(x*log(x),x=0,complex);

You can also compute limits as x $\rightarrow$ $\infty$ and limits of functions of more than one variable:

> 
  limit(arctan(x),x=infinity);

> 
  limit(x/(x^2+y^2),x=0,y=0);

A common error is to try to compute the limit of a function f(x) when x has been previously given a value. If you find yourself in this situation, unassign the value of x executing the command x:='x';. The previous example will fail if y still has the value assigned to it in section 4.2.