Plotting with Maple

Let us now use the graphics facilities of Maple:

> 
  plot(x^2, x=-10..10);

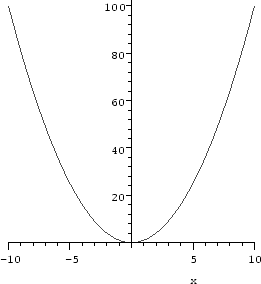
$\begin{mfigure}\centerline{ \psfig {figure=BFig3.ps,height=2.5in}}\end{mfigure}$

Maple displays the graph of the function x² from x = - 10 to x = 10 as requested. In the worksheet interface, clicking the right mouse button on the graph pops up a menu with various options which allow you to manipulate your graph, and/or change its appearance in a suitable way. Clicking the left button ``selects'' the graphic, drawing a black box with ``handles'' around it. You can drag the mouse button on these to resize the plot. Also, the coordinates of the point where you clicked appear in the upper left of the worksheet. Selecting a graphic also changes the context bar: shortcuts for manipulating the axes, aspect ratio, and plotting style appear as buttons along the top.

The basic syntax of the plot command is

> 
  plot(f,range);

where f is the expression to be plotted and range is the range of the parameter(s) for which you would like to see the plot of f. In the example above, we indicated the range of x by x=-10..10. Maple automatically chooses a scale on the vertical axis. There are many options to the plot command; while we will mention a few of them, the on-line help system has all the details.

Try both of the two similar plot commands below:

> 
  plot(x^2-x, x=-1..2, y=-1..2);
  plot(x^2-x, x=-1..2,   -1..2);

In both cases, the plot is displayed for values of y between -1 and 2, but in the first, the variable y is explicitly named in the command, and the vertical axis gets a label. Whenever you are plotting an expression, the variable in the domain of the function must be specified.

Plotting several functions (or curves) on the same axes

We can plot more than one function (or curve) on the same coordinate system. Consider the following example, recalling the slope function of the line passing through the points (x₁, y₁), (x₂, y₂), used to define the slope m(x) of the line passing through (1, 1) and (x, x²):

> 
  slope:=(x1,y1,x2,y2)->(y2-y1)/(x2-x1);
  m:=x->slope(1,1,x,x^2);

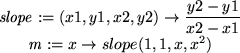
$\begin{maplelatex} \begin{displaymath}\mathit{slope} := (x1, y1, x2, y2) \righta... ...h}\mathit{m} := x \rightarrow slope(1,1,x,x^2) \end{displaymath}\end{maplelatex}$

We now define the equation of the lines passing through (1, 1) and (x, x²) for x = 2, 3, 4, 5 and plot the four lines together with the function x^2.

> 
  line1:=m(2)*(x-1)+1;
  line2:=m(3)*(x-1)+1; 
  line3:=m(4)*(x-1)+1; 
  line4:=m(5)*(x-1)+1; 
  plot(x^2,line1,line2,line3,line4,x=-3..6);

$\begin{maplelatex} \begin{displaymath}line1 := 3 x - 2 \end{displaymath}\begin{d... ...isplaymath}\begin{displaymath}line4 := 6 x - 5 \end{displaymath}\end{maplelatex}$

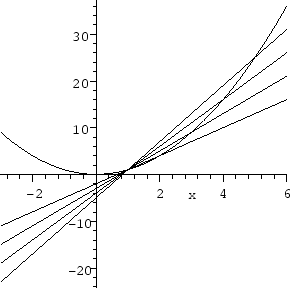
$\begin{mfigure}\centerline{ \psfig {figure=BFig4.ps,height=2.5in}}\end{mfigure}$

Observe that the expressions to be plotted are enclosed in braces { }. Besides specifying the range on which x varies as done above, you can also specify and label the y range proceeding exactly in the same manner as when plotting a single function.^1.13

Fancier plotting

The plot command is very powerful, and you should look for details about it using the online help facility; the command ?plot will bring this up. There are also several related pages, and some instructive example worksheets that are well worth looking at.

To make you aware of some of its features, we will discuss a few of them here:

It is possible to have Maple plot points. This can be done in two ways depending upon how the points are generated. If you have a list of specific points, you can assign them to a name and then plot them as follows:
```
> 
  points:=[[1,2],[1.5,1],[2,-1],[2.5,0.5],[3,1],[3.5,0.6],[4,0.2]]:
  plot(points,style=POINT);
```
If style=POINT is replaced by style=LINE, the dots will be connected by segments of lines. In the worksheet interface, you can switch from one style to the other by first clicking the left mouse button on the graph, and then hitting the relevant button on the buttonbar.
On the other hand, if the points result from evaluating an expression at several values of x, you can use plot in its usual form, but specifying style=POINT:
```
> 
  plot(x^2,x=-2..2,style=POINT);
```
Approximately 50 points will be plotted this way. You may notice that they will not usually be equally spaced, but concentrated in areas where the graph curves more. You can insist that more points be plotted by using the numpoints option:
```
> 
  plot(x^2,x=-2..2,style=POINT,numpoints=150);
```
Several more specialized plotting functions are contained in a separate library called plots. For basic plotting, there are two commands from this library that are especially useful. They are textplot and display. To load these commands into the computer memory, execute the statement
```
> 
  with(plots,textplot,display);
```
$\begin{maplelatex}[display,textplot] \end{maplelatex}$
The display command is useful to combine different kinds of plots into one picture. You can merge standard plots of expressions, plots of points, plots of text (This is the utility of textplot: to label things), and animations. In the next example, we combine the point plot of the variable points defined above with a plot of sin(3*x). We first define them as different plots and then display them together. Note that except for the third command, we end with a colon (:) in order to suppress the Maple output.
```
> 
  plot1:=plot([points],style=POINT):
  plot2:=plot(sin(3*x),x=0..4):
  display(plot1,plot2,view=[0..4,-1..2]);
```
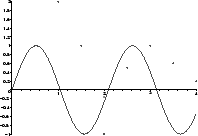
$\begin{mfigure}\centerline{\psfig{figure=BFig7.ps,width=2in,angle=270}}\end{mfigure}$

The view option controls the horizontal and vertical ranges to be displayed.
You can attach labels to your plots by combining textplot with display. The basic syntax of textplot is to use it with an argument of the form [a,b,'name'] which places the word name inside the quotes on the plot so that it is centered at the point (a, b). For example:
```
> 
  y:=(1+x^2)*exp(-x^2/2): d:=diff(y,x):
  F:=plot(y,d,x=-3..3):
  G:=textplot([1,1,'function'],[0.75,0.45,'derivative']):
  display(F,G);
```
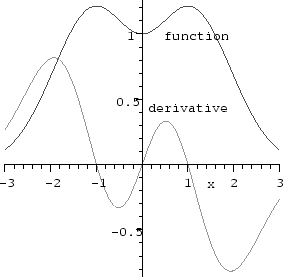
$\begin{mfigure}\centerline{ \psfig {figure=BFig5.ps,height=2.4in}}\end{mfigure}$

We end with a word about plotting functions (as opposed to expressions), and a situation in which it is a good idea to do so. Sometimes you will have a relationship that you want to plot in the form of a function rather than an expression:

> 
  f:=x->x^3*exp(-x):

In this situation, you can plot f(x) as explained above. Alternatively, you may use:

> 
  plot(f, 0..3);

The two ways of plotting a function should not be confused. Neither of the following two statements will work correctly:

> 
  plot(f(x), 0..3);

$\begin{maplettyout} Plotting error, empty plot \end{maplettyout}$

> 
  plot(f, x=0..3);

As you see, the first gives an error; the second gives a plot with nothing plotted on it.

If you have a function defined using an if-then clause, you must use the function plotting command:

> 
  f:=x-> if x<3 then x+1 else -x^2+13 fi:
  plot(f(x),x=0..5);

$\begin{maplettyout} Error, (in f) cannot evaluate boolean \end{maplettyout}$

The error resulted because Maple attempts to understand the expression f(x) before it has a value for x. One way around this^1.14is to use the command

> 
  plot(f, 0..5);

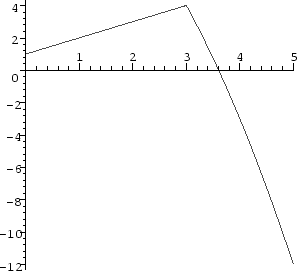
$\begin{mfigure}\centerline{ \psfig {figure=BFig6.ps,height=2.4in}}\end{mfigure}$

You can see from the graph that the function f is probably continuous but not differentiable at x=3.

Footnotes

... function.^1.13: We could have done this all in a single plot command, either explicitly typing each of the lines, or using seq to generate them: plot({x^2, seq( m(i)*(x-1)+1, i=2..5)}, x=-3..6);
... this ^1.14: We could also delay evaluation of f(x) using quotes, with plot('f(x)', x=0..5);. Alternatively, we could define f using piecewise, as f:=x-> piecewise(x<3, x+1, -x^2+13);.

Next: Exercises Up: Preliminaries about Maple Previous: The subs command

Translated from LaTeX by Scott Sutherland
2002-08-29