f (x) = 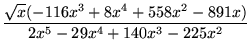 .
.
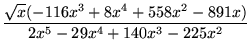 .
.
- a)
- Write this in a simpler form (that is, factor and reduce it).
- b)
- Draw the graph of the function for x between 0 and 1). Adjust the vertical range so that some detail can be seen.
- c)
- Compute the area of the part of the curve that lies above the x-axis and between x = 0 and x = 5 (that is, integrate the function over the appropriate range of x values). Give your answer both in actual form and as a decimal approximation to about 10 places.
- d)
- What is the value of the integral if you remove the factor of
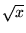 from the numerator?
from the numerator?
- e)
- Use the derivative of f (x) to determine for what real value x the function has a local maximum. Use an approximation to about 8 decimal places.
seq and ithprime to generate a list
of the first 20 primes. Compute the sum of these 20 primes, and give its
integer factors.
Hint: use a variation of the command
convert(taylor(cos(x),x,5),polynom) to make this work.
Think of a suitable way to demonstrate that the approximation you have taken is good.