Correlation functions

The way path integrals are used in quantum field theory is, very roughly speaking, that the probability amplitude of a process going from point $v_1$ to point $v_2$ is an integral over all possible ways of getting from $v_1$ to $v_2$. In our finite-dimensional model, each of these ``ways'' is represented by a point ${\bf v}$ in ${\bf R}^d$, and the probability measure assigned to that way is $\frac{1}{Z_U}\exp(-{\scriptstyle\frac{1}{2}}{\bf v}^tA~{\bf v} +\hbar U({\bf v}))v^1v^2~d{\bf v}$. The integral is then what we called before a 2-point function

$$\< v^1,v^2\> = \frac{1}{Z_U}\int_{{\bf R}^d}d{\bf v}~ \exp(-{\scriptstyle\frac{1}{2}}{\bf v}^tA~{\bf v} +\hbar U({\bf v}))v^1v^2,$$

and what we will now call a correlation function.

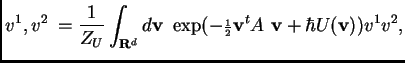
We continue with the example of the cubic potential

$$U({\bf v}) = \frac{1}{3!}\sum_{i,j,k} u_{ijk}v^iv^jv^k$$

. By our previous calculations,

$$\< v^1,v^2\> = \frac{1}{Z_U}\partial_1\partial_2 \exp(\hbar \sum_... ...iptstyle\frac{1}{2}}{\bf b}^tA^{-1}{\bf b})) _{\textstyle \vert _{{\bf b} =0}}.$$

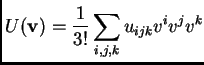
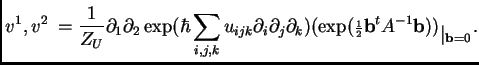
In terms of Wick's Theorem and our graph interpretation of pairings, this becomes:

$$\sum_G \frac{\textstyle \hbar^n}{\textstyle \vert{\rm Aut~}G\vert... ... edge~labellings} \prod_v u_{\rm vertex~label} \prod_e A^{-1}_{\rm edge~label},$$

where now the sum is over all graphs $G$ with two single-valent vertices (the ends) labeled 1,2 and $n$ 3-valent vertices.

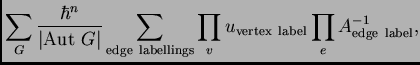
Here is a typical graph occurring in the calculation of the coefficient of $\hbar^6$ in $\< v^1,v^2\>$.

$k$-point correlation functions are similarly defined and calculated. Here is where we begin to see the usual ``Feynman diagrams.''

Here is a graph occurring in the calculation of the coefficient of $\hbar^2$ in $\< v^1,v^2,v^3,v^4\>$.