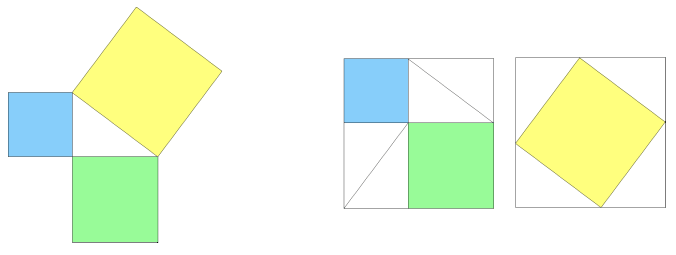


The theorem states that the yellow square (``the square on the hypothenuse'') is equal to the green square plus the blue square; this should become clear upon contemplation of the two compound squares on the right.
This proof is unusual in its brevity and its complete appropriateness to the problem. Pictures and diagrams are also used in non-geometrical parts of mathematics, mostly for psychological reasons: harnessing our ability to reason ``visually'' with the elements of a diagram in order to assist our more purely logical or analytical thought processes.
Some diagrams are more useful than others. Edward R. Tufte has written three books analyzing the effectiveness of figures and diagrams in communicating ideas. His latest,Visual Explanations -Images and Quantities, Evidence and Narrative (Graphics Press, Cheshire CT 1997) was reviewed in the January 1999 AMS Notices by Bill Casselman of the University of British Columbia. Casselman focusses on the applications of Tufte's ideas to explanations in mathematics, and distills from the book a set of rules designed to make graphics contribute most effectively to the communication of mathematics.
Tufte's Rules, after Casselman, abridged:
--Tony Phillips
SUNY at Stony Brook