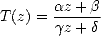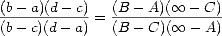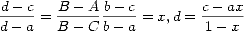A new solution to the three body problem - and more

by Bill Casselman

3. The triangle construction

In order to explain what Chenciner and Montgomery have (and haven't) proven, I need to include a short digression about the topological nature of the system.

Richard Moeckel was apparently the first to suggest that a relatively simple but effective way to understand what is going on topologically is to track the triangle whose vertices are located at the centers of the three bodies. With any legitimate choreography orbit, the bodies following the path will avoid collisions, which means that at any moment all three of the sides of this triangle will have non-zero length. It turns out to be useful to focus attention on the shapes of the triangles, that is to say, to consider similar triangles as being equivalent. Furthermore, it is useful to keep track of labels for the vertices. There is a very pretty way to parametrize such configurations.

We are interested in parametrizing labeled configurations of three points ABC in the Euclidean plane, which we identify with the plane of complex numbers, such that at least one of the sides has non-zero length. Such a configuration will be called here a labeled triangle. Two such configurations ABC and A^*B^*C^* will be called equivalent if the map taking A to A^* etc. is a similarity (so the labeling is an important part of the structure). Fix one particular labeled triangle abc to be the equilateral triangle in the complex plane with vertices at the cube roots of unity, lettering counter-clockwise starting with 1.

Now some complex analyis. If ABC is a triangle with all vertices distinct, there exists a unique Möbius transformation

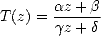
taking ABC to abc. Then the map associating to ABC the image d under T of the point at infinity extends to all labeled triangles, and establishes a bijection between the space of equivalence classes of non-singular triangles and the points of the Riemann sphere (the complex plane together with the point at infinity). The easiest way to find that complex number d is to solve this equation, which expresses that the cross-ratio of four points is invariant under Möbius transformations.

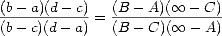
We get

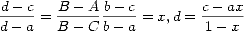
The equation shows that a positively oriented equilateral triangle corresponds to the point at infinity; this is because for such a triangle x=1; similarly a triangle with A=B maps to the point c, a triangle with A=C to the point b, a triangle with B=C to the point a. This is the important point for us: the triangles formed by a collisionless choreography will always lie in the complement of a, b and c. Furthermore positively oriented triangles map to the outside of the unit circle, where |d| > 1; degenerate triangles, with all vertices on a line, map to the unit circle; and negatively oriented ones to the inside, with a negatively oriented equilateral triangle going to 0.

If we are given any periodic collisionless system of three bodies, as they move the point corresponding to the triangle they form will trace out a path in the complement, on the Riemann sphere, of a, b, and c. The homotopy class of this path is a strong topological invariant of the system. In a Lagrangian system, the three bodies always form an equilateral triangle, although it may grow, shrink, or rotate. Thus Lagrangian systems map to 0 or to infinity, the two poles of the Riemann sphere. The Eulerian systems map to points on the unit circle (its equator). One gets a feel for the complexity of a system by constructing its path traced out on the Riemann sphere by the triangle the bodies bound. Here is what happens for the figure eight:

The Möbius transformation maps a labeled triangle ABC to a point on the Riemann sphere (the complex plane together with a point at infinity), where we have singled out the three cube roots of 1: a=1, b, c, in counterclockwise order. Triangles with A=C map to the point b, etc., so the triangles formed by a collisionless choreography will always lie in the complement of a=1, b, and c. Positively oriented triangles map outside the unit circle, negatively oriented ones inside, triangles with the three vertices collinear map to the circle itself. Isosceles triangles map to one of three lines running through the origin and a=1, b, or c. Similar (and similarly labeled) triangles map to the same point on the Riemann sphere.

The principal result of Chenciner and Montgomery is that in the homotopy class of the track of the path exhibited above there does exist the track of a three-body system.