e-MATH
Metonymy and Metaphor in Mathematics


 
 

Metaphors from modern mathematics:

I. Fourier analysis and the dot-product

Metonymy is everywhere in mathematics, but a good metaphor is hard to find. This one and the next are two of my favorites.

In the simplest form of Fourier analysis, the calculation of the Fourier sine series for an odd function f(x) defined on $[-\pi,\pi]$, the function is represented as a linear combination of the functions $ \sin(x), \sin(2x), \sin(3x),$ etc.

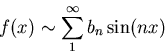
\begin{displaymath}f(x) \sim \sum_1^{\infty}b_n \sin(nx)\end{displaymath}

where the coefficients b1, b2, etc. are given by the integrals


\begin{displaymath}b_n =\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)\sin(nx)~ dx\end{displaymath}



The metaphier. In ${\bf R}^3$, a vector ${\bf v}$ can be represented as a linear combination of the basis elements ${\bf i},{\bf j},{\bf k}$:


\begin{displaymath}{\bf v} = b_1{\bf i} + b_2{\bf j} + b_3{\bf k}\end{displaymath}

where the coefficients b1, b2, etc. are given by the dot products


\begin{displaymath}b_1 = {\bf v}\cdot{\bf i}, b_2 = {\bf v}\cdot{\bf j}, b_3 = {\bf v}\cdot{\bf k}.\end{displaymath}

This works because the basis ${\bf i},{\bf j},{\bf k}$ is orthonormal:

\begin{displaymath}{\bf i}\cdot{\bf j} = 0,~ {\bf i}\cdot{\bf k} = 0,~ {\bf j}\cdot{\bf k} =0\end{displaymath}


\begin{displaymath}{\bf i}\cdot{\bf i} = 1,~ {\bf j}\cdot{\bf j} = 1,~ {\bf k}\cdot{\bf k} =1.\end{displaymath}



The metaphor: in the vector space of piecewise-smooth, odd functions on $[-\pi,\pi]$, define


\begin{displaymath}f\cdot g = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x)g(x)~ dx.\end{displaymath}

Then the functions $\sin(x), \sin(2x), \sin(3x), \dots$ are orthonormal with respect to this dot-product, as can be checked by carrying out the integrals. So writing the Fourier sine series for f is exactly analogous to writing v as a linear combination of ${\bf i},{\bf j},{\bf k}$ using the dot-products as coefficients.

(For more details see a text like David Powers, Boundary Value Problems Academic Press, New York 1972 or Walter Rudin, Principles of Mathematical Analysis McGraw Hill, New York 1974.)


© copyright 1999, American Mathematical Society.