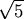e-MATH
The most irrational number


 
 

The most irrational number

The most irrational number turns out to be a number already well known in geometry. It is the number

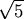g = (sqr5 + 1)/2 = 1.618033...

which is the length of the diagonal in a regular pentagon of side length 1. This number, known as the "golden mean," has played a large role in mathematical aesthetics. It is not clear whether its supreme irrationality has anything to do with its artistic applications.

The golden mean satisfies the equation x2 - x - 1 = 0, so its continued fraction expansion is the simplest of all: 


g = 1 + 1
       ------
       1 + 1
          ------
          1 + 1
             ------
             1 + etc.

Its convergents are 1, 2, 3/2, 5/3, 8/5, ... , the ratios of consecutive Fibonacci numbers.

How well are these convergents approximating g? Here are the first few E/M ratios: 

convergent   E/M
c1 =  1/1     1.382
c2 =  2/1     .8541
c3 =  3/2     1.055
c4 =  5/3     .9787
c5 =  8/5     1.008
c6 =  13/8    .9968
c7 =  21/13   1.001
c8 =  34/21   .9995 
...
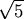Hurwitz' Theorem guarantees the existence of infinitely many convergents with E/M < 1. In this case the odd-numbered convergents must be discarded, and the even-numbered ones are getting as bad as they can be. (In fact this table is evidence that the factor sqr5 in Hurwitz' theorem cannot be improved!)

So the golden mean can never have a rational approximation as good as 22/7 was for pi or even as good as 7/5 was for sqr2.

On to next irrational page.

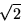Back to previous irrational page.

Back to first irrational page.


© copyright 1999, American Mathematical Society.