Where do the "best" rational approximations come from?

The "best" rational approximations, as well as most of the theory of rational approximation, arise from continued fraction expansions.

A continued fraction expansion for a positive number x is a sequence of positive integers a₁,a₂,a₃, ... such that x is the limit of the rational numbers:

c1 = a1

c2 = a1 +  1
          ---
           a2


c3 = a1 +  1
         -------
         a2 + 1
             ---
              a3

c4 =  a1 +  1
          -------
          a2 + 1
              -------
               a3 + 1
                   ---
                    a4 


c5 = etc.

 
Any rational number p/q which approximates x to within 1/2q2 
must be one of the convergents of x.

In terms of our table, this means that any rational approximation with E/M < 1.118.. must be a convergent.

Calculating a continued fraction expansion

• From the decimal expansion. If we know the number well enough, for example to enough decimal places, we can calculate its continued fraction expansion as we show here with x = = 3.14159265359...

  The point is to make c₁, c₂, c₃, etc. alternately smaller and larger than x by choosing the largest possible a₁, a₂, a₃, etc.

  • a₁ is the integer part, here 3. This is the largest integer which makes c₁ less than .

  • With a₁ = 3, a₂ is the largest integer which makes c₂ greater than .
    8 is too large because 3 + 1/8 = 3.125... < ,
    but 7 makes it since 3 + 1/7 = 3.1428.. > .
    So a₂ = 7, and c₂ = 3 + 1/7 = 22/7.

  • With a₁ = 3 and a₂ = 7, a₃ is the largest integer which makes c₃ less than .
    16 is too large because 3 + 1/(7+1/16) = 3.14159292... > ,
    but 15 works since 3+1/(7+1/15) = 3.1415094... < .
    So a₃ = 15, and c₃ = 3+1/(7+1/15) = 333/106.

  • Continue, alternating "greater" and "less." You should find a₄ = 1 and a₅ = 292. More a's will require more decimal places.

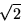• If the number is a root of a quadratic equation ax² - bx - c = 0 with b strictly positive, and a = c = 1, the equation yields an algorithm for generating the continued fraction expansion. itself does not work, but x=1+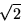 is a root of x²-2x-1=0. The equation can be rewritten as x=2+1/x. Substituting the right hand side into itself gives x = 2+1/(2+1/x), and then x = 2+1/(2+1/(2+1/x)) etc. Since 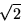= (1+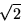) - 1, the procedure yields for 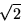the continued fraction expansion:

      
           1 +  1
               -------
                2 + 1
                   -------
                    2 + 1
                       -------
                        2 + 1
                           -------
                            2 + etc.
  

  and the convergents for 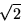are c₁= 1, c₂= 3/2, c₃ = 7/5, c₄ = 17/12, c₅ = 41/29, c₆ = 99/70, c₇ = 239/169, ...

Back to previous irrational page.

Back to first irrational page.