
The mathematical CAT scan
1. A numerical simulation
Each image in a CAT scan is produced from a collection of 1-dimensional
X-ray projections, taken from different angles in the same plane. Typically,
the object to be scanned lies through the center of a large, vertical doughnut;
the X-ray source and the X-ray detector rotate inside the
doughnut, one opposite the other. For each angle sampled, the detector
gives a 1-dimensional X-ray record: it sweeps across and
registers, at each position, how much radiation is getting through.
This gives, for each angle, a 1-dimensional picture which can be interpreted
as a graph of the X-ray penetrability of the object along a family
of lines at that
angle.
In a CAT scan the information we want is a 2-dimensional picture:
what the X-ray penetrability is at each point of a planar cross-section
through the object. The information we get is a collection of
1-dimensional records, each one giving the X-ray penetrability
of the object along a family of parallel lines. The mathematical
operation that allows the reconstruction of a function of two
variables from the knowledge of its totals along lines is called
the Radon Transform. In more mathematical terms,
the principle of the Radon Transform is that function of two variables can
be reconstructed if its integral is known along any line in its domain.
In terms of approximations,
it can be reconstructed to a given degree of accuracy
if these integrals are known for an appropriately dense family of lines.
Here is a crude but illustrative example.
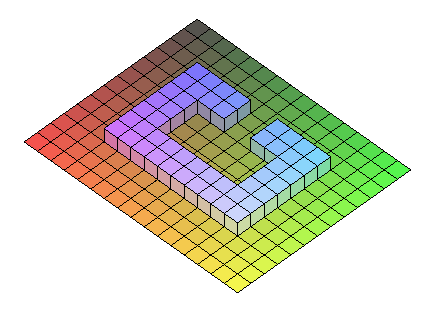
A two-dimensional ``object'' is constructed on a grid by blacking out
a certain number of squares. We can think of this as assigning density
1 to the blackened squares and density 0 to the others. A shape like
the letter ``C,'' for instance, can be given by the following pattern
of 0s and 1s. This density function can be represented by a 3-dimensional
graph, as shown on the right.
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0
0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0
0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0
0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0
0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
|
 |
The integral of the density along a line in the domain
can be represented here by adding up the number of ones
hit by a line through the grid. Instead of taking all
possible lines, we will take eight families defined
by the grid. The rows of the grid give one family. For
this family the sums are 0,0,0,8,8,4,4,4,10,10,0,0,0
as we move down through the grid. The columns of the
grid give a second family, with sums 0,0,0,7,7,4,4,2,2,7,7,0,0
as we scan from left to right. Two more families are
given by the diagonal lines in the grid. For example, the upward diagonal
starting at the lower left corner has sum 3, while
the downward diagonal starting at the upper left corner has
sum 4. The remaining four families are given by the
lines in the grid of slope 2, -2, 1/2 and -1/2. A line
of slope 2 goes over one square and up 2 at each step,
and a line of slope -1/2 goes over 2 and down 1 at each step.
For example, the line of slope -2 through the upper left corner
of the grid has sum 2. (If this grid were a chess board, the
families would correspond to straight-line moves by rooks,
bishops and knights.)
These eight families of lines are illustrated in this table:
each family is labelled by its slope, and each line is
labelled by the number of ones it intercepted in the
object. In each family
one of those lines is picked put in red.
horizontal X stands for 10
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0_0_0_0 0 0 0_0_0_0 0 0 0
8 8 8|8 8 8 8|8 8|8 8 8 8|8 8 8
8 8 8|8 8_8_8|8 8|8_8_8 8|8 8 8
4 4 4|4 4|4 4 4 4 4 4|4 4|4 4 4
4 4 4|4 4|4 4 4 4 4 4|4 4|4 4 4
4 4 4|4 4|4_4_4_4_4_4|4 4|4 4 4
X X X|X X X X X X X X X X|X X X
X X X|X_X_X_X_X_X_X_X_X_X|X X X
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
|
slope = 1/2
0 0 0 0 0 0 0 0 0 1 1 2 2 2 2 2
0 0 0 0 0 0 0 1 1 2 2 2 2 2 2 3
0 0 0 0_0_1_1 2 2 2_2_2_2 3 3 2
0 0 0|1 1 2 2|2 2|2 2 3 3|2 2 3
0 1 1|2 2_2_2|2 2|3_3_2 2|3 3 3
1 2 2|2 2|2 2 3 3 2 2|3 3|3 3 3
2 2 2|2 2|3 3 2 2 3 3|3 3|3 3 2
2 2 2|3 3|2_2_3_3_3_3|3 3|2 2 1
2 3 3|2 2 3 3 3 3 3 3|2 2|1 1 0
3 2 2|3_3_3_3_3_3_2_2_1_1|0 0 0
2 3 3 3 3 3 3 2 2 1 1 0 0 0 0 0
3 3 3 3 3 2 2 1 1 0 0 0 0 0 0 0
3 3 3 2 2 1 1 0 0 0 0 0 0 0 0 0
|
slope = 1
0 0 0 0 0 0 1 2 3 4 3 2 3 4 4 4
0 0 0 0 0 1 2 3 4 3 2 3 4 4 4 4
0 0 0 0_1_2_3 4 3 2_3_4_4 4 4 4
0 0 0|1 2 3 4|3 2|3 4 4 4|4 4 4
0 0 1|2 3_4_3|2 3|4_4_4 4|4 4 3
0 1 2|3 4|3 2 3 4 4 4|4 4|4 3 2
1 2 3|4 3|2 3 4 4 4 4|4 4|3 2 1
2 3 4|3 2|3_4_4_4_4_4|4 3|2 1 0
3 4 3|2 3 4 4 4 4 4 4 3 2|1 0 0
4 3 2|3_4_4_4_4_4_4_3_2_1|0 0 0
3 2 3 4 4 4 4 4 4 3 2 1 0 0 0 0
2 3 4 4 4 4 4 4 3 2 1 0 0 0 0 0
3 4 4 4 4 4 4 3 2 1 0 0 0 0 0 0
|
slope = 2
0 0 0 0 0 1 2 3 2 1 1 2 2 2 3 2
0 0 0 0 1 2 3 3 1 1 2 2 2 3 3 2
0 0 0 0_1_2_3 2 1 1_2_2_2 3 2 1
0 0 0|1 2 3 3|1 1|2 2 2 3|3 2 1
0 0 0|1 2_3_2|1 1|2_2_2 3|2 1 0
0 0 1|2 3|3 1 1 2 2 2|3 2|1 0 0
0 0 1|2 3|2 1 1 2 2 2|3 2|1 0 0
0 1 2|3 3|1_1_2_2_2_3|3 2|1 0 0
0 1 2|3 2 1 1 2 2 2 3 2 1|0 0 0
1 2 3|3_1_1_2_2_2_3_3_2_1|0 0 0
1 2 3 2 1 1 2 2 2 3 2 1 0 0 0 0
2 3 3 1 1 2 2 2 3 3 2 1 0 0 0 0
2 3 2 1 1 2 2 2 3 2 1 0 0 0 0 0
|
vertical
0 0 0 7 7 4 4 2 2 4 4 7 7 0 0 0
0 0 0 7 7 4 4 2 2 4 4 7 7 0 0 0
0 0 0 7_7_4_4 2 2 4_4_7_7 0 0 0
0 0 0|7 7 4 4|2 2|4 4 7 7|0 0 0
0 0 0|7 7_4_4|2 2|4_4_7 7|0 0 0
0 0 0|7 7|4 4 2 2 4 4|7 7|0 0 0
0 0 0|7 7|4 4 2 2 4 4|7 7|0 0 0
0 0 0|7 7|4_4_2_2_4_4|7 7|0 0 0
0 0 0|7 7 4 4 2 2 4 4 7 7|0 0 0
0 0 0|7_7_4_4_2_2_4_4_7_7|0 0 0
0 0 0 7 7 4 4 2 2 4 4 7 7 0 0 0
0 0 0 7 7 4 4 2 2 4 4 7 7 0 0 0
0 0 0 7 7 4 4 2 2 4 4 7 7 0 0 0
|
slope = -2
2 3 2 2 2 1 1 2 3 2 1 0 0 0 0 0
2 3 3 2 2 2 1 1 3 3 2 1 0 0 0 0
1 2 3 2_2_2_1 1 2 3_2_1_0 0 0 0
1 2 3|3 2 2 2|1 1|3 3 2 1|0 0 0
0 1 2|3 2_2_2|1 1|2_3_2 1|0 0 0
0 1 2|3 3|2 2 2 1 1 3|3 2|1 0 0
0 0 1|2 3|2 2 2 1 1 2|3 2|1 0 0
0 0 1|2 3|3_2_2_2_1_1|3 3|2 1 0
0 0 0|1 2 3 2 2 2 1 1 2 3|2 1 0
0 0 0|1_2_3_3_2_2_2_1_1_3|3 2 1
0 0 0 0 1 2 3 2 2 2 1 1 2 3 2 1
0 0 0 0 1 2 3 3 2 2 2 1 1 3 3 2
0 0 0 0 0 1 2 3 2 2 2 1 1 2 3 2
|
slope = -1
4 4 4 3 2 3 4 3 2 1 0 0 0 0 0 0
4 4 4 4 3 2 3 4 3 2 1 0 0 0 0 0
4 4 4 4_4_3_2 3 4 3_2_1_0 0 0 0
4 4 4|4 4 4 3|2 3|4 3 2 1|0 0 0
3 4 4|4 4_4_4|3 2|3_4_3 2|1 0 0
2 3 4|4 4|4 4 4 3 2 3|4 3|2 1 0
1 2 3|4 4|4 4 4 4 3 2|3 4|3 2 1
0 1 2|3 4|4_4_4_4_4_3|2 3|4 3 2
0 0 1|2 3 4 4 4 4 4 4 3 2|3 4 3
0 0 0|1_2_3_4_4_4_4_4_4_3|2 3 4
0 0 0 0 1 2 3 4 4 4 4 4 4 3 2 3
0 0 0 0 0 1 2 3 4 4 4 4 4 4 3 2
0 0 0 0 0 0 1 2 3 4 4 4 4 4 4 3
|
slope = -1/2
2 2 2 2 2 1 1 0 0 0 0 0 0 0 0 0
3 2 2 2 2 2 2 1 1 0 0 0 0 0 0 0
2 3 3 2_2_2_2 2 2 1_1_0_0 0 0 0
3 2 2|3 3 2 2|2 2|2 2 1 1|0 0 0
3 3 3|2 2_3_3|2 2|2_2_2 2|1 1 0
3 3 3|3 3|2 2 3 3 2 2|2 2|2 2 1
2 3 3|3 3|3 3 2 2 3 3|2 2|2 2 2
1 2 2|3 3|3_3_3_3_2_2|3 3|2 2 2
0 1 1|2 2 3 3 3 3 3 3 2 2|3 3 2
0 0 0|1_1_2_2_3_3_3_3_3_3|2 2 3
0 0 0 0 0 1 1 2 2 3 3 3 3 3 3 2
0 0 0 0 0 0 0 1 1 2 2 3 3 3 3 3
0 0 0 0 0 0 0 0 0 1 1 2 2 3 3 3
|
Comments: webmaster@ams.org
© copyright 1999, American Mathematical Society.

