|
The simplest example of a catastrophe, mathematically speaking,
occurs in the system consisting of a ball free to roll under gravity
in a double-well container that can be tilted from one side to
the other. Here the input is the tilt of the container, and the
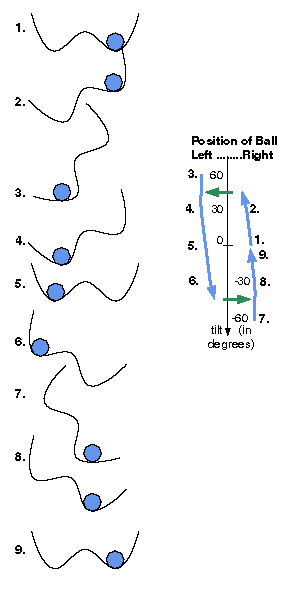
output is the position of the ball. There is one catastrophe just beyond the configuration labelled 2. in the figure and on the graph. This is the point where the ball is just poised to fall to the left, but is still balanced on the right side of the well. If the ball is exactly at that point, the tiniest additional tilt will cause a large displacement of the ball (green arrow). A symmetrical catastrophe is just beyond the configuration labelled 6. The catastrophe in this system is a one-parameter, or "co-dimension 1" catastrophe: there is one controlling variable, namely the tilt of the well. Other mathematical catastrophes share an important feature of this system: the output is determined by a mechanism (in this case, gravity acting on the ball) that seeks the lowest possible position compatible with the constraint (in this case, staying in the well). The work of classifying mathematical catastrophes was done in the 1960's and 1970's. Together with its applications, it gave rise to "Catastrophe Theory." For example, it is known that any one-parameter catastrophe must be, qualitatively, exactly like the green arrow. This is called the Fold Catastrophe. In this column, we will investigate the only two-parameter catastrophe, the Cusp Catastrophe, and illustrate it with an ingenious machine invented and popularized by Christopher Zeeman. |