Spherical Tetrahedra with Vertices in the Binary Tetrahedral Group

There are 12 geometrically distinct tetrahedra with vertices in the binary tetrahedral group. Conformal images of three of them are shown here. The first is the simplest: the generalized octant (hexadecant?) AAAA with volume 1/16 of the total volume. Here it is positioned with its vertices at 1,i,j,-k. The second is the largest, ADDD, with volume almost 1/4 the total volume. Here it is shown with vertices i,j,k,a^2. The third is the smallest, BBEE, shown here with vertices i,j,d,-a^2; its volume is barely more than 1/100 the total volume. These images were produced using GeomView modules developed by Geometry Center Summer Institute student Rebecca Frankel of MIT. Larger versions of these images, with more detailed explanations, can be reached through links below.

NOTATION: Edge lengths and dihedral angles are encoded as before:
p = pi/2, g = pi/3, b = v = 2*pi/3,
with in addition
h = pi/4, i = 3*pi/4.
In the table below each row corresponds to a single 3-simplex type. (Note that the set of faces determines the simplex up to a mirror-symmetry). In the first column each simplex is assigned a 1-letter code. In the second column the simplexes are listed lexicographically for convenience in reference. In the third column the list of faces is rewritten in a more topological order

In the fourth column the six edge lengths of those faces are recorded, in the order 01,02,03,12,13,23 (referring to the vertices in the following copy of the diagram)

                        0
                        /\
                       /  \
                      1----2
                     / \  / \
                    /   \/   \
                   0-----3----0

In the fifth column the six dihedrals are recorded, in the same order, except that the first one is the dihedral opposite 01, etc. These dihedrals were calculated as in Vinberg's paper. The sixth column records the relative frequency of each simplex: (1/24) times the number each occurred in an enumeration of all simplexes of the form 1,x,y,z. The seventh column records the volume relative to the total volume of SU(2). See Calculation of Volumes for the explanation of how these volumes were computed.

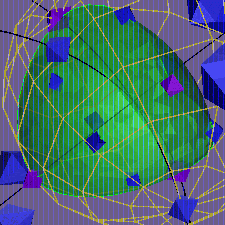
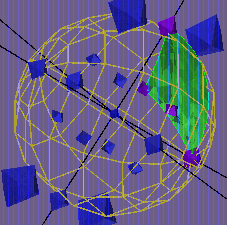
Highlighted symbols link to conformal images of the tetrahedra in SU(2), prepared with GeomView modules developed by Rebecca Frankel.


Code  Lexic. Topol.  Edges  Dihedrals  Rel.Freq.  Volume

K      AAAA   AAAA  pppppp    pppppp      2        1/16
O      ABBB   BBAB  gggppp    hhhbbb      8        1/64
N      ABCC   BCAC  ggbppp    hhibgg     24        5/192
M      ACCD   DCAC  bbgppp    iihbgg     24        11/192
L      ADDD   DDAD  bbbppp    iiibbb      8        15/64
Q      BBCC   CBBC* gbppgg    gbppgg     24        1/48
V      BBEE   BEBE  gggpgg    ggpbgg     12        1/96
S      BDFF   DFBF  bbbpgg    bbpbgg     24        7/96
P      CCDD   CDCD* bpbgpb    bpbgpb     24        5/48
U      CCEF   ECCF* ggbgpb    gpbggb     24        1/32
T      CCFF   FCCF* bbggpb    bpgggb     24        5/96
R      DDFF   DFDF  bbgpbb    bbpbbb     12        17/96
       BBBB   BBBB  ggppgg  (singular**)  3          0
       BCCD   DCBC  bbppgg  (singular**) 12          0
       CCCC   CCCC  bpggpb  (singular**)  6          0
       DDDD   DDDD  bbppbb  (singular***) 3         1/2

* occur in non-congruent mirror-image pairs.
** these three have volume zero, corresponding to the decompositions B+B=B+B, D=B+2*C, C+C=C+C respectively;
*** this degenerate tetrahedron has all dihedrals equal to pi, and encloses one-half the volume of the 3-sphere.

Back to Binary Tetrahedral Main Page
Back to Tony's Home Page

Tony Phillips
tony@math.sunysb.edu
March 26 1997