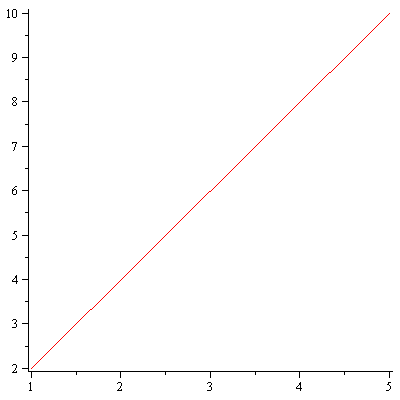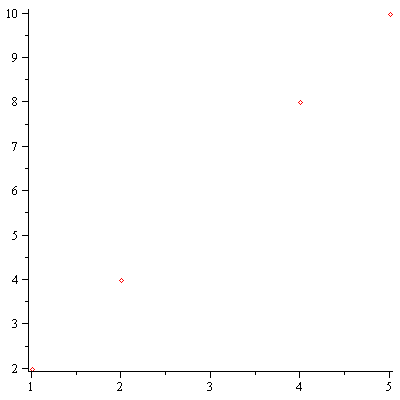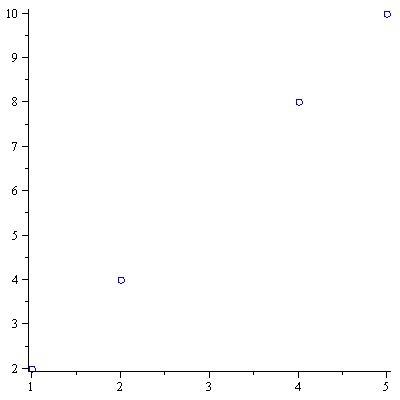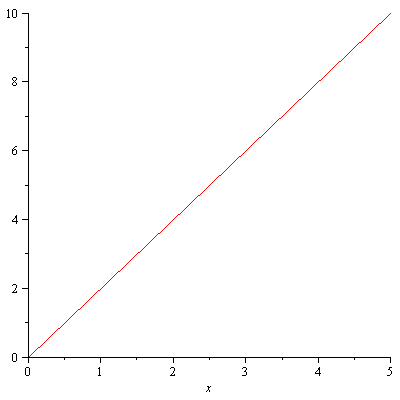>

 

I forgot to save the worksheet on this day, so I'm trying to recreate it from memory. Sorry about that.  Here goes: 

First, we were talking about lists and sets and data and points and so on.  Sets are surrounded by {} braces and have no inherent order.  A list is surrounded by [] and has a fixed order. 

>

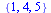{1,5,4};

 

(1)

 

>

[1,5,4];

 

(2)

 

Both lists and sets can have anything inside them, including another set or list: 

>	{ 1, [4,5], 2, {3}, apple};

 

(3)

 

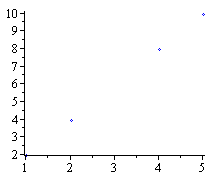
We can represent a point in the plane as a pair of numbers.  Here we have a list of points: 

>	data := [ [1,2], [2,4], [4,8], [5,10]];

 

(4)

 

>	plot(data);

 

>	plot(data,style=point);

 

>	plot(data,style=point,symbolsize=15,symbol=circle,color=blue);

 

>	plot(2*x,x=0..5);

 

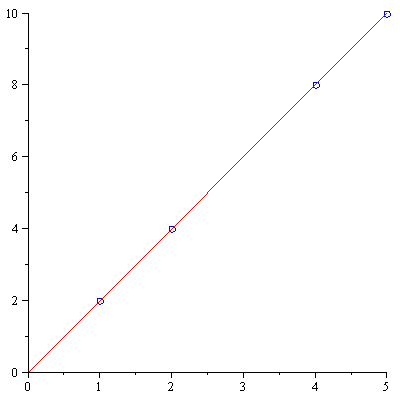
We'd like to see both the line and the points on the same graph.  We can do this by assigning the plots to a variable, and then using the display command from the plots library to show them on the same plot. 

>	linepic:=plot(2*x,x=0..5): pointpic:=plot(data,style=point,symbolsize=15,symbol=circle,color=blue):

 

>

pointpic;

 

>	plots[display]({linepic,pointpic});

 

Let's generate some data, and let maple find the appropriate line for us.  We'll use the seq command, so first let's play with the command itself. 

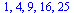>	seq(i^2,i=1..5);

 

(5)

 

>	seq([i,i^2],i=1..5);

 

(6)

 

Now let's make some points on the line y=x/2 

>	pts:=[seq([x,x/2],x=0..10)];

 

(7)

 

>	with(CurveFitting);

 

(8)

 

>	PolynomialInterpolation(pts,x);

 

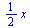(9)

 

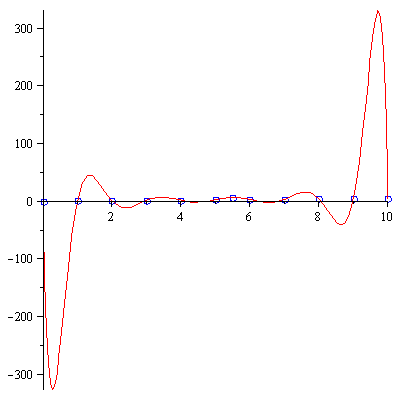
>	pts2:=[seq([x,x/2],x=0..5),[5.5,6.5],seq([x,x/2],x=6..10)];

 

(10)

 

>	PolynomialInterpolation(pts2,x);

 

(11)

 

>	with(plots):

 

>	display(  [plot(pts2,style=point,symbolsize=15,symbol=circle,color=blue),   plot(PolynomialInterpolation(pts2,x),x=0..10)]);

 

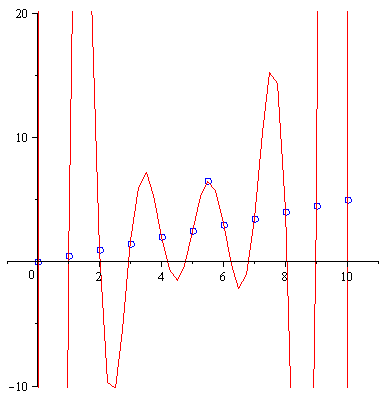
>	display(  [plot(pts2,style=point,symbolsize=15,symbol=circle,color=blue),   plot(PolynomialInterpolation(pts2,x),x=-1..11,y=-10..20)]);

 

>