- Our vectors, which we denote as usual by greek letters
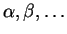 , are the positive real numbers,
, are the positive real numbers, 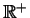 .
.
- Our field of scalars (denoted by roman letters
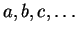 )
can be either the reals
)
can be either the reals 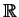 or the rationals
or the rationals 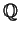 . We'll write
. We'll write 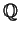 but
we get a vector space with
but
we get a vector space with 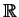 as well.
as well.
- To ``add'' two vectors, we multiply the corresponding real numbers.
That is, the vector sum of
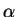 and
and 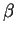 is the product
is the product
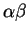 .
.
- The scalar product of a scalar
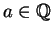 and the vector
and the vector
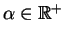 , we compute the power
, we compute the power 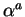 .
.
Let's check that this satisfies the necessary properties:
- additive closure
- If
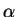 and
and 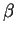 are positive real numbers,
so is their product
are positive real numbers,
so is their product 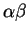 .
.
- associativity of addition
- Multiplication of real numbers is associative, so no problem.
- commutivity of addition
- Multiplication of real numbers is commutative.
- additive identity
- The positive real number 1 acts as the identity
element for vector addition, since
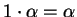 .
.
- additive inverses
- For any vector
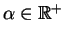 , there is another
vector
, there is another
vector
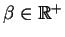 so when the two vectors are ``added'', the result
is the identity element above. In this case, the inverse of
so when the two vectors are ``added'', the result
is the identity element above. In this case, the inverse of 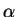 is
is
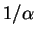 , since
, since
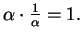
- closure of scalar multiplication
- For any scalar
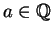 and any
vector
and any
vector
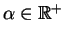 , the scalar multiple
, the scalar multiple 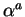 is still in
is still in 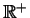 .
.
- neutrality of 1
- When we compute the scalar multiple of the
multiplicative identity in our field
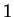 with any vector
with any vector
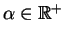 ,
we should get the original vector. That works fine:
,
we should get the original vector. That works fine:
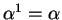
- vector distributive law
- Multiplying a scalar
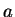 times the sum of two
vectors
times the sum of two
vectors 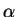 and
and 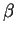 :
:
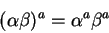
- scalar distributive law
- The sum of two scalars
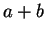 times a vector
times a vector
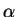 :
:
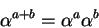
So we see that ![]() is a vector space over
is a vector space over ![]() , with an appropriate
interpretation of vector addition and scalar multiplication.
, with an appropriate
interpretation of vector addition and scalar multiplication.
Note also that in this case, a ``linear combination'' works out to be very
like factoring. For example, we can express the vector ![]() as a linear
combination of the vectors
as a linear
combination of the vectors ![]() and
and ![]() by
by
Note that there may be more than one way to express the same vector as a
linear combination of two others. For example, if our underlying field is
![]() , then there are scalars in
, then there are scalars in ![]() equal to
equal to ![]() and
and ![]() , and
so
, and
so
is also a scalar. But then if we have
we also have
since
More concretely, since
we also have
So we can express
The situation is more complicated if we consider ![]() as a vector space
over
as a vector space
over ![]() , since
, since
![]() will be rational for some
will be rational for some
![]() and
and ![]() , and not for others. What do you think the dimension
of this vector space is?
, and not for others. What do you think the dimension
of this vector space is?