We now turn to a brief discussion of area. Rather than carefully developing this theory, we shall begin with some ``obvious'' facts, such as
The Pythagorean Theorem, relating the lengths of the legs of a right
triangle to the length of the hypotenuse, is very well-known; you've
probably seen it repeatedly since your elementary school days, and
know it quite well.
The figure on the left below is sometimes described as a proof of the
Pythagorean Theorem, but in fact it is much closer to a geometric
statement of the theorem. To turn it into a proof requires
constructing a number of additional lines, and a fairly complex
argument. On left is the figure for Euclid's proof, sometimes called
``the bride's chair''. We won't give the argument
here, but you might try to figure it out on your own. The idea is to
show that there are two pairs of congruent triangles, and the area of each
triangle in a pair is half of one of the smaller squares. The sum of
the areas in the pairs gives the area of the larger square.
There are many proofs of this theorem; we know of at least 40. Below we give one of the simpler ones. It is necessary to use the Parallel Axiom (Axiom 8) axiom, either implicitly or explicitly, in order to prove the Pythagorean Theorem; the theorem is false in both spherical and hyperbolic geometry, which have a different version of Axiom 8. Surprisingly, the Pythagorean Theorem is equivalent to this axiom; that is, the Parallel Axiom can be proven if we assume the Pythagorean Theorem first.
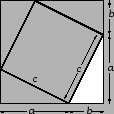
In addition, there is an inner quadrilateral formed whose sides are the
hypotenuse of each of the triangles. This quadrilateral is certainly a
rhombus, because each side is of length ![]() . But it is in fact a square,
because each of its angles are right: at each vertex there are three angles
which sum to an angle of measure
. But it is in fact a square,
because each of its angles are right: at each vertex there are three angles
which sum to an angle of measure ![]() . Two of these are the acute angles in
a right triangle, and so the third must be of measure
. Two of these are the acute angles in
a right triangle, and so the third must be of measure ![]() .
.
The area of the outer square is ![]() , the area of each of the four
triangles is
, the area of each of the four
triangles is
![]() , and the area of the inner square is
, and the area of the inner square is ![]() .
Thus, we have
.
Thus, we have
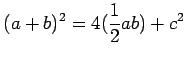
From this, we readily see that
![]() .
.
![]()
Since the sum of the measures of a triangle is constant, if we are given two
triangles,
![]() and
and
![]() , and we know that
, and we know that
![]() , and
, and
![]() , then the triangles are similar.
, then the triangles are similar.
If the triangles are similar, we write
![]() .
.
We want to prove the very useful fact that the side lengths of similar
triangles are proportional. However, this is easier to do if we
first prove it for right triangles, and then apply this result to the
general case.
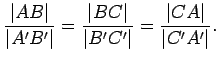
Let ![]() be a line parallel to
be a line parallel to ![]() that meets
that meets ![]() at the point
at the point ![]() where
where
![]() . Denote the point where
. Denote the point where ![]() meets
meets ![]() by
by
![]() . Let
. Let ![]() be the line through
be the line through ![]() parallel to
parallel to ![]() , and let
, and let ![]() be the line perpendicular to
be the line perpendicular to ![]() at
at ![]() . Then, since
. Then, since ![]() and
and ![]() are both perpendicular to
are both perpendicular to ![]() , they are parallel. Let
, they are parallel. Let ![]() be the
point of intersection of
be the
point of intersection of ![]() with
with ![]() . Then
. Then ![]() is a
rectangle. Also, let
is a
rectangle. Also, let ![]() be the point of intersection of
be the point of intersection of ![]() and
and
![]() . Finally, let
. Finally, let ![]() be the line perpendicular to
be the line perpendicular to ![]() and
and ![]() through
through ![]() ; denote the point of intersection of
; denote the point of intersection of ![]() with
with ![]() by
by ![]() and
denote the point of intersection of
and
denote the point of intersection of ![]() with
with ![]() by
by ![]() .
.
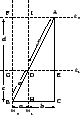
The line ![]() divides the rectangle
divides the rectangle ![]() into two congruent triangles.
Since the areas of
into two congruent triangles.
Since the areas of
![]() and
and
![]() are equal, and the
areas of
are equal, and the
areas of
![]() and
and
![]() are equal, we obtain that the
areas of the two smaller rectangles are equal; that is,
are equal, we obtain that the
areas of the two smaller rectangles are equal; that is, ![]() .
.
Since we drew the line ![]() parallel to
parallel to ![]() , we know that
, we know that
![]() . So, for this case, our theorem, which we want to
prove, says that
. So, for this case, our theorem, which we want to
prove, says that
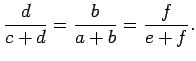
To see that the first of these inequalities is true, notice that it
holds when
![]() (by cross multiplying). But this holds
since we have already established that
(by cross multiplying). But this holds
since we have already established that ![]() .
.
We check that the second equality is true by using the first equality
together with the Pythagorean theorem. That is, we write
![]() and
and
![]() , and then, as above, cross-multiply and use the
two facts that we have already proven; namely that
, and then, as above, cross-multiply and use the
two facts that we have already proven; namely that ![]() , and that
, and that
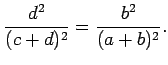
Now since
![]() , we have
, we have
![]() and
and
![]() . Since
. Since ![]() is parallel to
is parallel to
![]() ,
,
![]() (using alternate interior angles and
vertical angles). Since
(using alternate interior angles and
vertical angles). Since
![]() by construction,
by construction,
![]() via ASA.
Using the above, we conclude that
via ASA.
Using the above, we conclude that
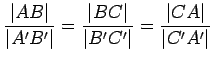
Now that we have shown the desired property for right triangles, we can use that result to show it for arbitrary similar triangles.
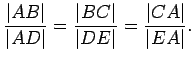
Let ![]() be the altitude from
be the altitude from ![]() , and let
, and let ![]() be the point of
intersection of
be the point of
intersection of ![]() with the line
with the line ![]() . Then
. Then ![]() and
and ![]() are
similar right triangles, and
are
similar right triangles, and ![]() and
and ![]() are similar right
triangles. Hence the proportion theorem for right triangles yields
are similar right
triangles. Hence the proportion theorem for right triangles yields
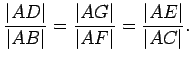
That
![]() follows easily from the
Lemma above.
follows easily from the
Lemma above.
![]()
In what follows, we will deliberately confuse an angle with its
measure; i.e., we will not distinguish between ![]() and
and ![]() . It should always be clear from the context which is meant.
. It should always be clear from the context which is meant.
We note that it is almost immediate from the definition that
In order to extend the definitions to all values of ![]() , first we set
, first we set
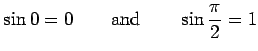
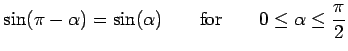
We can then use the fact that
![]() and
and
![]() to extend the definitions of the other
functions to all real numbers (except those where we would need to divide by
0, such as for
to extend the definitions of the other
functions to all real numbers (except those where we would need to divide by
0, such as for
![]() .
.
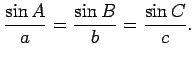
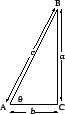
Now let ![]() be an arbitrary triangle, where
be an arbitrary triangle, where ![]() and
and ![]() are acute angles
(i.e., their measures are less than
are acute angles
(i.e., their measures are less than ![]() ),
and let
),
and let ![]() be the altitude from
be the altitude from ![]() . Then
. Then
![]() , and
, and
![]() . Hence
. Hence
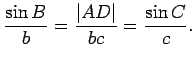
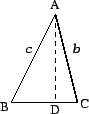
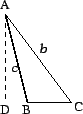
If angle ![]() is obtuse, repeat the above argument, exchanging
is obtuse, repeat the above argument, exchanging ![]() and
and ![]() .
.
The other equality follows by looking at the altitude from ![]() and/or
and/or ![]() .
.
![]()
We next take up the case that ![]() is obtuse. In this case, the
endpoint of the altitude
is obtuse. In this case, the
endpoint of the altitude ![]() is such that
is such that ![]() lies between
lies between ![]() and
and
![]() . Similar to the above, we set
. Similar to the above, we set ![]() . Then the Pythorean
theorem yields the following.
. Then the Pythorean
theorem yields the following.
One can easily prove these theorems by constructing
![]() ,
where
,
where
![]() , and the altitude from
, and the altitude from ![]() divides
this triangle into two triangles,
divides
this triangle into two triangles,
![]() and
and
![]() ,
in such a way that
,
in such a way that
![]() and
and
![]() . Then,
using the definitions of the sine and cosine for right triangles, the
addition formula for the sine follows from the law of sines, and the
addition formula for the cosine follows from the Pythagorean theorem
and the law of cosines.
. Then,
using the definitions of the sine and cosine for right triangles, the
addition formula for the sine follows from the law of sines, and the
addition formula for the cosine follows from the Pythagorean theorem
and the law of cosines.
We can use the laws of sines and cosines to obtain information about
triangles.