

Next: 2 Triangles and congruence
Up: MAT 200 Course Notes on
Previous: MAT 200 Course Notes on
Subsections
What is a triangle? Is a triangle a physical
object made up of 3 straight pieces of wood or metal or somesuch, joined
at the corners, or is it an ideal object consisting of lines that have no
width lying in a plane that has no thickness?
Historically, all lengths and
angles are somehow constructible. That is, they are abstract objects that,
in some sense are capable of being realized as physical objects. We will
take a somewhat different point of view; we will assume familiarity with
real numbers, and with the correspondence between real numbers and points on
a line.
The plane, lines, points, length and distance,
angle measure.
- Points lie on lines.
- If two distinct points lie on a line, then the length of the line segment
between these points is well defined.
- A point separates a line into two half-lines.
- Two distinct points on the same line separate it into a line segment,
which has a length (the length is a positive number), and two half-lines.
- A line separates the plane into two half-planes, which are regions (in
modern terms, a region is a connected open subset of the plane).
- Two distinct lines either meet at a
point, or are disjoint, in which case they are parallel.
These are the first few; a few more will
follow. The reader should be aware that the numbering of the axioms, as
well as the theorems, propositions, etc. is unique to these notes. It is
also possible to have the same notion of planar geometry with a slightly
different collection of axioms, but these are what we shall use.
Axiom 1
Two distinct lines intersect in at most one point.
Axiom 2
Any two distinct points lie on a line.
Axiom 3
If two lines intersect in a point, they separate the
plane into 4 regions, called sectors, and they define an angle in
each of these sectors; the sum of the measures of any two adjacent angles is
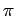 .
.
Axiom 4
If two lines do not intersect, they divide the plane
into three regions, with exactly one of them, the one between the two lines,
having both lines on its boundary.
Exercise 1.1
Using the above axioms, show that given any two distinct points, there is
exactly one line that contains them both.
If  and
and  are distinct points, then the (unique) line on which
they lie is denoted by
are distinct points, then the (unique) line on which
they lie is denoted by  . The line segment between
. The line segment between  and
and  is
also denoted by
is
also denoted by  ; this should cause no confusion.
The length of the line segment
; this should cause no confusion.
The length of the line segment  is denoted by
is denoted by 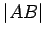 .
.
If  and
and 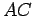 are distinct lines or line segments, the angle between them
is denoted by
are distinct lines or line segments, the angle between them
is denoted by
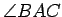 , and its measure is denoted by
, and its measure is denoted by
 . We may use
. We may use 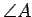 to denote an angle which has the point
to denote an angle which has the point
 at its vertex, if it is clear from the context which angle is
being referred to. It is also not unusual to use Greek letters such as
at its vertex, if it is clear from the context which angle is
being referred to. It is also not unusual to use Greek letters such as
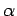 ,
, 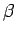 ,
, 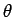 ,
, 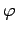 , etc. to denote both angles and
their measures.
, etc. to denote both angles and
their measures.
Theorem 1.1 (Vertical angles)
Vertical angles are equal. That is, if two distinct lines
intersect at a point, the measure of the angles of any two non-adjacent
sectors is equal.
Exercise 1.2
Prove Thm. 1.1. You may use any of the axioms above,
along with logical axioms and results for real numbers (since angle
measure is a real number).
(more will follow)
- Any line segment can be extended in either direction, or in both
directions.
- If
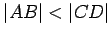 , then there is a point
, then there is a point 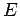 on the line
on the line 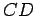 , where
, where 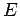 lies between
lies between  and
and  , so that
, so that 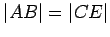 (see also Axiom
(see also Axiom ![[*]](crossref.gif) ).
).
- If
 and
and  are points on the line
are points on the line  , and we are
given an angle
, and we are
given an angle
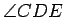 , where
, where
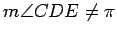 , then we can
construct points
, then we can
construct points 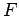 and
and 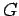 , one on each side of the line
, one on each side of the line 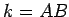 , so that
, so that
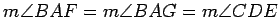 .
(see also Axiom
.
(see also Axiom ![[*]](crossref.gif) ).
).


Next: 2 Triangles and congruence
Up: MAT 200 Course Notes on
Previous: MAT 200 Course Notes on
Scott Sutherland
2002-12-18
![]() and
and ![]() are distinct lines or line segments, the angle between them
is denoted by
are distinct lines or line segments, the angle between them
is denoted by
![]() , and its measure is denoted by
, and its measure is denoted by
![]() . We may use
. We may use ![]() to denote an angle which has the point
to denote an angle which has the point
![]() at its vertex, if it is clear from the context which angle is
being referred to. It is also not unusual to use Greek letters such as
at its vertex, if it is clear from the context which angle is
being referred to. It is also not unusual to use Greek letters such as
![]() ,
, ![]() ,
, ![]() ,
, ![]() , etc. to denote both angles and
their measures.
, etc. to denote both angles and
their measures.
![[*]](crossref.gif) ).
).
![[*]](crossref.gif) ).
).