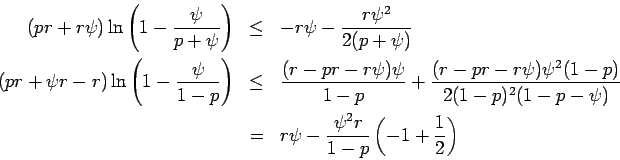Next: The magic of sampling
Up: Probabilistic Encryption
Previous: The Goldwasser-Micali encryption system
Contents
Both the encryption algorithm and the hypothetical algorithms used by
the adversary involve random events. We will need a theorem that says
that, if an event with probability  is tried
is tried 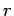 times, the chance that
the number of successes is not close to
times, the chance that
the number of successes is not close to 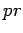 is small. The paper uses7(p. 293)
is small. The paper uses7(p. 293)
Lemma 24
Let  be the number of successes in
be the number of successes in 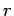 tries.
For any
tries.
For any 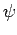
Proof: 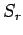 is a random variable, which is the sum of
is a random variable, which is the sum of 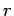 independent random variables, each having value 0 or 1. Let
independent random variables, each having value 0 or 1. Let 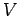 be the
variance of
be the
variance of 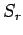 . Each of the 0-1 variables has variance
. Each of the 0-1 variables has variance 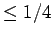 ,
so
,
so
Lemma 24 provides a very rough estimate of the probability.
An improvement requiring much more work is:
For comparison, if 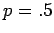 ,
, 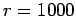 , the probability that there are
, the probability that there are
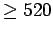 successes is .1087. Lemma 24 gives8an upper limit of .3125,
while Lemma 25 gives .1498. (these figures courtesy of
Mathematica)
successes is .1087. Lemma 24 gives8an upper limit of .3125,
while Lemma 25 gives .1498. (these figures courtesy of
Mathematica)
One reason the paper does not
use Lemma 25 is that it does not give a simple formula for
how large 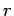 would have to be in terms of the other quantities. We will
not use this result later, and you should skip to section 7.3
unless you like to manipulate formulas.
would have to be in terms of the other quantities. We will
not use this result later, and you should skip to section 7.3
unless you like to manipulate formulas.
Proof: We will assume 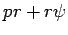 is integer.
From the binomial theorem:
is integer.
From the binomial theorem:
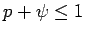 implies
implies 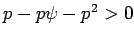 and
and
which gives the second factor of 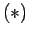 . We
use Stirling's formula on the binomial coefficient and group it with the
powers of
. We
use Stirling's formula on the binomial coefficient and group it with the
powers of  and
and 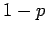 to obtain:
to obtain:
The first factor of 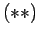 is the first factor of
is the first factor of 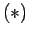 . We
obtain upper bounds on the rest of
. We
obtain upper bounds on the rest of 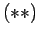 , using
, using
(the lower bound on 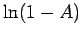 involves a geometric series)
involves a geometric series)
Adding these and using 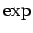 gives the remaining factor of
gives the remaining factor of 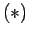 .
.
Footnotes
- ... uses7
- The usual central limit theorem cannot be used because it does
not tell you how large
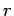 must be for the normal distribution to give
a good estimate.
must be for the normal distribution to give
a good estimate.
- ... gives8
- We divide by 2 to eliminate the probability of
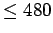 .
.




Next: The magic of sampling
Up: Probabilistic Encryption
Previous: The Goldwasser-Micali encryption system
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
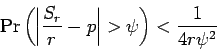
![]() is a random variable, which is the sum of
is a random variable, which is the sum of ![]() independent random variables, each having value 0 or 1. Let
independent random variables, each having value 0 or 1. Let ![]() be the
variance of
be the
variance of ![]() . Each of the 0-1 variables has variance
. Each of the 0-1 variables has variance ![]() ,
so
,
so ![]() ,
, ![]() , the probability that there are
, the probability that there are
![]() successes is .1087. Lemma 24 gives8an upper limit of .3125,
while Lemma 25 gives .1498. (these figures courtesy of
Mathematica)
successes is .1087. Lemma 24 gives8an upper limit of .3125,
while Lemma 25 gives .1498. (these figures courtesy of
Mathematica)
![]() would have to be in terms of the other quantities. We will
not use this result later, and you should skip to section 7.3
unless you like to manipulate formulas.
would have to be in terms of the other quantities. We will
not use this result later, and you should skip to section 7.3
unless you like to manipulate formulas.
![]() is integer.
From the binomial theorem:
is integer.
From the binomial theorem: