



Next: Encryption techniques based on
Up: Introduction to Number Theory
Previous: Primitive roots
Contents
Proof of Theorem 5
This proof unfortunately requires many lemmas.
It is probably a good idea to skip over
the lemmas as much as possible on a first reading.
We begin with three preliminary results about greatest common
divisors, which may be intuitive.
Proof: By Theorem 1, there are integers 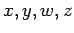 with
with
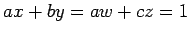 . Together these imply
. Together these imply
which is impossible if 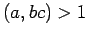 . height 8pt width 4pt
. height 8pt width 4pt
Lemma 12
If  divides
divides 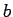 and
and 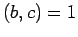 , then
, then 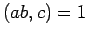 .
.
Proof: Let 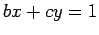 and
and 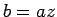 . Then
. Then
Lemma 13
If 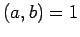 ,
, 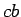 is divisible by
is divisible by  , and
, and 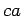 is
divisible by
is
divisible by 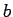 , then
, then 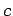 is divisible by
is divisible by 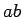 .
.
Proof: Let 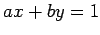 ,
, 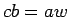 , and
, and 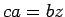 . Then
. Then
The key step of the proof begins with any
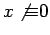 . Let
. Let 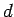 be the smallest positive number for which
be the smallest positive number for which 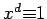 (there must be such a
(there must be such a 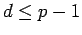 since
since
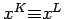 implies
implies
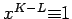 ). By Lemma 10,
if
). By Lemma 10,
if 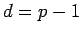 ,
, 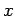 is a primitive root. If
is a primitive root. If 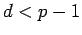 , we will
find
, we will
find 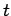 with
with
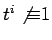 for all
for all 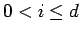 . If
. If 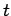 is not a
primitive root, we repeat the process, this time with
is not a
primitive root, we repeat the process, this time with 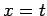 . Since
the exponent
. Since
the exponent 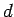 increases each time, we eventually obtain a
primitive root.
increases each time, we eventually obtain a
primitive root.
Proof: This can be proved in
the same way as the corresponding theorem in ordinary algebra: if 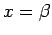 is a solution, the polynomial can be written as
is a solution, the polynomial can be written as 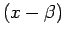 times a polynomial of degree
times a polynomial of degree 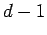 , which by induction has
, which by induction has 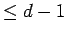 solutions. height 8pt width 4pt
solutions. height 8pt width 4pt
We return to the proof of Theorem 5.2 The sequence
consists of 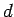 different solutions
of
different solutions
of 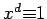 . If
. If 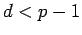 ,
let
,
let
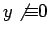 be any non-member of the sequence,
with
be any non-member of the sequence,
with 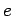 the smallest positive number with
the smallest positive number with 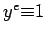 .
If
.
If 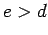 , we may take
, we may take 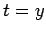 , so we will assume
, so we will assume 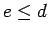 from now on.
By Lemma 14,
from now on.
By Lemma 14,
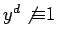 , which implies
, which implies 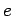 does not divide
does not divide
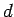 and
and 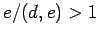 . We will use
. We will use 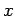 and
and 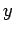 to construct a number
to construct a number
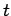 such that
such that
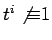 for all
for all 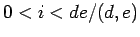 . The construction
is based on two lemmas:
. The construction
is based on two lemmas:
Lemma 15
Suppose that 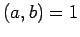 and that
and that 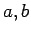 are the smallest
positive numbers for which
are the smallest
positive numbers for which
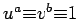 . If
. If 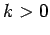 and
and
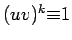 , then
, then 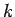 is divisible by
is divisible by 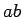 .
.
Proof: Since
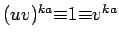 , Lemma 9
implies
, Lemma 9
implies 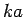 is divisible by
is divisible by 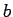 . Similarly
. Similarly 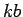 is divisible by
is divisible by  ,
and Lemma 13 gives the desired result. height 8pt width 4pt
,
and Lemma 13 gives the desired result. height 8pt width 4pt
Lemma 16
Let 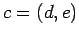 ,
, 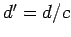 ,
, 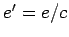 .
There are
.
There are 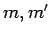 such that
(i)
such that
(i) 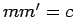 and (ii)
and (ii) 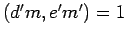 .
.
Proof:
Let 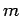 be the largest divisor of
be the largest divisor of 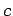 for which
for which 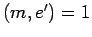 ,
, 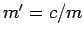 .
The maximality of
.
The maximality of 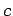 implies
implies 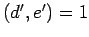 .
By Lemma 11,
.
By Lemma 11, 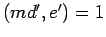 .
.
The maximality of 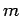 and Lemma 12
implies
and Lemma 12
implies 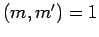 . Since
. Since 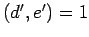 implies
implies
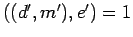 , Lemma 11 implies
, Lemma 11 implies
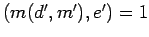 . Thus
the maximality of
. Thus
the maximality of 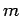 implies
implies 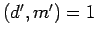 . Lemma 11 now implies
. Lemma 11 now implies
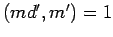 .
.
Applying Lemma 11 to the conclusions of the
preceding paragraphs yields 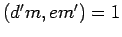 . height 8pt width 4pt
. height 8pt width 4pt
We can finally complete the proof of Theorem 5.
With the notation of Lemma 16, let 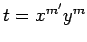 . For
. For 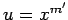 ,
,
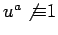 for
for 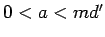 . A similar assertion holds for
. A similar assertion holds for 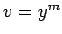 .
The other conditions of Lemma 15 are satisfied, and we can
conclude that
.
The other conditions of Lemma 15 are satisfied, and we can
conclude that 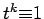 if and only if
if and only if 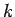 is a multiple of
is a multiple of
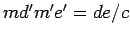 . height 8pt width 4pt
. height 8pt width 4pt
This proof does not give us an efficient procedure for finding
a primitive root for large primes  , but the reason may not be obvious.
The steps implicit in the lemmas can all be carried out efficiently.
The one problem is the choice of
, but the reason may not be obvious.
The steps implicit in the lemmas can all be carried out efficiently.
The one problem is the choice of 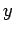 , which was required to be
a non-member of the set of powers of
, which was required to be
a non-member of the set of powers of 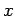 . It is too inefficient to
list all the powers of
. It is too inefficient to
list all the powers of 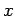 if
if 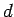 is large, and no significantly
better way of finding a non-member is known.
is large, and no significantly
better way of finding a non-member is known.
Footnotes
- ...proot.2
- This proof
uses ideas of Michael Fischer, who pointed out an error in an earlier
version.




Next: Encryption techniques based on
Up: Introduction to Number Theory
Previous: Primitive roots
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() . Let
. Let ![]() be the smallest positive number for which
be the smallest positive number for which ![]() (there must be such a
(there must be such a ![]() since
since
![]() implies
implies
![]() ). By Lemma 10,
if
). By Lemma 10,
if ![]() ,
, ![]() is a primitive root. If
is a primitive root. If ![]() , we will
find
, we will
find ![]() with
with
![]() for all
for all ![]() . If
. If ![]() is not a
primitive root, we repeat the process, this time with
is not a
primitive root, we repeat the process, this time with ![]() . Since
the exponent
. Since
the exponent ![]() increases each time, we eventually obtain a
primitive root.
increases each time, we eventually obtain a
primitive root.
![]() and Lemma 12
implies
and Lemma 12
implies ![]() . Since
. Since ![]() implies
implies
![]() , Lemma 11 implies
, Lemma 11 implies
![]() . Thus
the maximality of
. Thus
the maximality of ![]() implies
implies ![]() . Lemma 11 now implies
. Lemma 11 now implies
![]() .
.
![]() . height 8pt width 4pt
. height 8pt width 4pt
![]() . For
. For ![]() ,
,
![]() for
for ![]() . A similar assertion holds for
. A similar assertion holds for ![]() .
The other conditions of Lemma 15 are satisfied, and we can
conclude that
.
The other conditions of Lemma 15 are satisfied, and we can
conclude that ![]() if and only if
if and only if ![]() is a multiple of
is a multiple of
![]() . height 8pt width 4pt
. height 8pt width 4pt
![]() , but the reason may not be obvious.
The steps implicit in the lemmas can all be carried out efficiently.
The one problem is the choice of
, but the reason may not be obvious.
The steps implicit in the lemmas can all be carried out efficiently.
The one problem is the choice of ![]() , which was required to be
a non-member of the set of powers of
, which was required to be
a non-member of the set of powers of ![]() . It is too inefficient to
list all the powers of
. It is too inefficient to
list all the powers of ![]() if
if ![]() is large, and no significantly
better way of finding a non-member is known.
is large, and no significantly
better way of finding a non-member is known.