



Next: Construction of hard-core predicates
Up: Further results on pseudo-random
Previous: Further results on pseudo-random
Contents
We have seen several functions 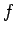 with the property that
with the property that 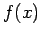 was easy to compute but
was easy to compute but 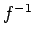 was difficult. Such an
was difficult. Such an 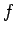 is called
a one-way function.16 A predicate
is a property
is called
a one-way function.16 A predicate
is a property 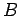 which is true or false for any
which is true or false for any 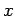 .
Typical examples might be ``is an odd number'' or ``is
.
Typical examples might be ``is an odd number'' or ``is 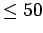 .''
A hard-core predicate for a function
.''
A hard-core predicate for a function 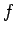 is a predicate
such that
is a predicate
such that
- there is an efficient algorithm for deciding whether
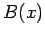 is
true
is
true
- if we are given
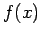 , there is no efficient algorithm
for guessing whether
, there is no efficient algorithm
for guessing whether 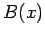 is true which has a probability much
greater than
is true which has a probability much
greater than 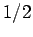 of being right.
of being right.
The example we used in the quadratic number generator was
where we are looking only at those 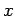 which are squares.
which are squares.
Theorem 32
If 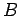 is a hard-core predicate for
is a hard-core predicate for 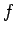 , the random number
generator in which a seed
, the random number
generator in which a seed 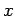 is chosen at random, giving the
sequence of bits
satisfies the Next Bit Condition.
is chosen at random, giving the
sequence of bits
satisfies the Next Bit Condition.
As a corollary,
the sequence 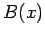 ,
, 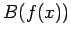 ,...satisfies all efficient tests,
using the arguments in the preceding section.
,...satisfies all efficient tests,
using the arguments in the preceding section.
Proof: If there were a program which took as input a sequence of bits and could guess the next bit, we could get a good
guess on 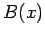 with
with 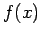 known
by asking the next-bit predictor what would
occur next in the sequence
known
by asking the next-bit predictor what would
occur next in the sequence
(this is really the same proof as
in the case of the quadratic generator).
Footnotes
- ... function.16
- In later work, we will be defining
a one-way function to be such that there is no efficiently computable
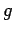 with
with
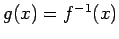 for most
for most 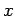 .
.




Next: Construction of hard-core predicates
Up: Further results on pseudo-random
Previous: Further results on pseudo-random
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() with
with ![]() known
by asking the next-bit predictor what would
occur next in the sequence
known
by asking the next-bit predictor what would
occur next in the sequence