


Next: A public key system
Up: Encryption techniques based on
Previous: The Diffie-Hellman key exchange
A sets up a system so that anyone can send him an encoded
message, but only A will be able to decode it. The message is represented
as a number 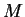 .
The encoding is done by a publicly known function
.
The encoding is done by a publicly known function 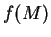 ,
with A the only person who knows how to compute
,
with A the only person who knows how to compute 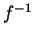 .
A chooses two large primes
.
A chooses two large primes 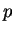 ,
,
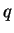 which he keeps secret. He announces
which he keeps secret. He announces
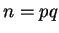 and another number
and another number 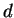 ,
with
,
with
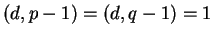 (one way to
do this is to choose
(one way to
do this is to choose 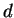 a prime larger than
a prime larger than 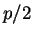 and
and 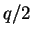 .)
The encoding is
.)
The encoding is
where 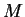 and
and 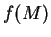 are both
are both 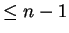 .
We have seen
.
We have seen 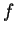 can be computed in a realistic amount of time
even if
can be computed in a realistic amount of time
even if 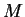 ,
,
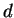 ,
,
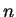 are many digits long.
are many digits long.
A computes 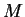 from
from 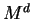 using his knowledge of
using his knowledge of 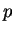 ,
,
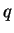 .
By
Corollary 8,
.
By
Corollary 8,
Similarly
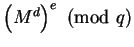 if
if
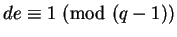 .
.
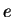 satisfies these two conditions if
satisfies these two conditions if
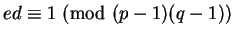 .
Theorem 1
says we can let
.
Theorem 1
says we can let 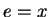 ,
where
,
where 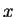 is a solution of
is a solution of
Since
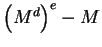 is divisible by
is divisible by 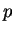 and by
and by 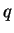 ,
it is
divisble by
,
it is
divisble by 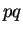 ,
hence we can recover
,
hence we can recover 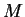 from
from 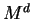 by taking to
the
by taking to
the 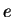 -th power mod
-th power mod 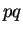 .
.
It is crucial to the security of this system that knowledge of
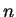 does not allow an eavesdropper to calculate
does not allow an eavesdropper to calculate 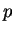 and
and 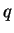 .
The
crude approach of dividing
.
The
crude approach of dividing 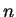 by all numbers up to
by all numbers up to 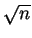 would
take
would
take
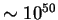 steps for a 100-digit
steps for a 100-digit 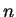 .
However, many famous
mathematicians have been unable to devise significantly better
factoring algorithms, and this problem has been studied for at
least 100 years.
.
However, many famous
mathematicians have been unable to devise significantly better
factoring algorithms, and this problem has been studied for at
least 100 years.
One practical difficulty in using this system is the need to
do calculations with many-digit numbers, especially to find primes.
Another difficulty is that the inventors of this system have patented
it. Amateur programmers who have posted implementations on electronic
bulletin boards have received letters from ``RSA Security, Inc''
warning of possible patent infringement.



Next: A public key system
Up: Encryption techniques based on
Previous: The Diffie-Hellman key exchange
Translated from LaTeX by Scott Sutherland
1998-03-15
![]() from
from ![]() using his knowledge of
using his knowledge of ![]() ,
,
![]() .
By
Corollary 8,
.
By
Corollary 8, ![]() does not allow an eavesdropper to calculate
does not allow an eavesdropper to calculate ![]() and
and ![]() .
The
crude approach of dividing
.
The
crude approach of dividing ![]() by all numbers up to
by all numbers up to ![]() would
take
would
take
![]() steps for a 100-digit
steps for a 100-digit ![]() .
However, many famous
mathematicians have been unable to devise significantly better
factoring algorithms, and this problem has been studied for at
least 100 years.
.
However, many famous
mathematicians have been unable to devise significantly better
factoring algorithms, and this problem has been studied for at
least 100 years.