


Next: Primitive roots
Up: Introduction to Number Theory
Previous: The Greatest Common Divisor
The sequence
has many applications in cryptography.
Before looking at theoretical properties, the example below (done
using a pocket calculator) should make clear that it is practical
to compute these numbers, even when many digits are involved.
Suppose we want to compute 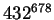 mod 987. The basic trick
is to start with a number and keep squaring:
mod 987. The basic trick
is to start with a number and keep squaring:
Since
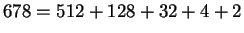 ,
,
Calculations with exponents
involve not-too-many multiplications. If the numbers have several
hundred digits, however, it is necessary to design special sub
routines to do the multiplications (see Knuth, volume 2).
Let us look at the sequence of powers of 2 mod 11:
Each number from 1 to 10 appears
in the sequence.
Theorem 5
Let
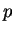
be a prime. There
is an
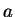
such that for every
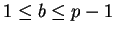
,
there is
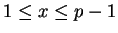
such that
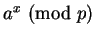
.
It is not always the case that 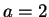 .
The powers of 2 mod 7 are
2, 4, 1 after which the sequence repeats and we never get 3, 5, or 6.
.
The powers of 2 mod 7 are
2, 4, 1 after which the sequence repeats and we never get 3, 5, or 6.
The proof of Theorem 5 is long, and we will give it in
section 2.5. For now, we want to look at some of its consequences.
Corollary 6
Let
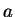
be as in Theorem
5. Then
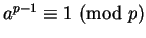
.
Proof: We know that
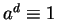 for some
for some
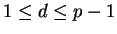 .
If
.
If
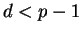 ,
the sequence of powers of
,
the sequence of powers of 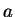 would start repeating before
we got all the numbers:
would start repeating before
we got all the numbers:
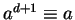 ,
,
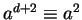 ,
etc.
height 8pt width 4pt
,
etc.
height 8pt width 4pt
Proof: Let 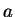 be
as in Theorem 5. Using Corollary 6
be
as in Theorem 5. Using Corollary 6
Corollary 8
If
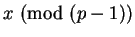
,
then
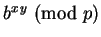
Proof: For some integer 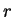 ,
,
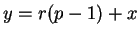 and by Corollary 7
and by Corollary 7
Lemma 9
Let
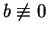
,
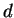
the smallest
positive number such that
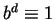
.
Then for any
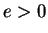
with
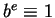
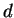
divides
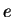
evenly. In particular, by Corollary
7,
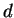
divides
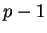
evenly.
Proof: If 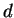 does not divide
does not divide 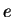 ,
then
,
then
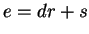 for some
for some 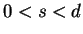 ,
but
,
but
would contradict the definition of 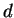 .
height 8pt width 4pt
.
height 8pt width 4pt



Next: Primitive roots
Up: Introduction to Number Theory
Previous: The Greatest Common Divisor
Translated from LaTeX by Scott Sutherland
1998-03-15
![]() mod 987. The basic trick
is to start with a number and keep squaring:
mod 987. The basic trick
is to start with a number and keep squaring: