


Next: A recent pseudo-random number
Up: Further results on pseudo-random
Previous: Hard-Core Predicates and Pseudo-Random
It seems much harder to find examples of hard-core predicates
than of one-way functions. The latter can be obtained from
discrete logarithms, subset-sum problems, and elsewhere.
It is difficult to prove that a property cannot be guessed
with probability much larger than 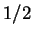 .
This makes the
following result17 interesting.
.
This makes the
following result17 interesting.
Theorem 33
Let
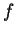
be a one-way function which maps sequences
of bits of length
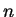
to sequences of length
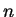
.
For each
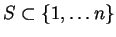
and
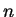
-bit
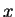
define
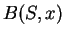
to be true if the number of 1's in positions in
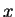
specified
by
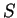
is even. There is no efficient algorithm which can guess
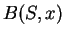
given
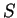
and
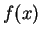
with probability much greater than
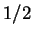
.
This result does not rule out the possibility that, for some
specific 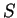 ,
it may be possible to guess
,
it may be possible to guess 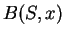 in an
efficient way. However, it would not be possible to do something like
guess
in an
efficient way. However, it would not be possible to do something like
guess 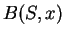 with probability
with probability 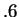 for
for 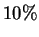 of all possible
of all possible 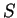 ,
and probability
,
and probability 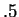 for all other
for all other 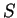 .
[this would imply we would
be correct about
.
[this would imply we would
be correct about 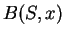 overall with probability
overall with probability 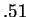 ]
]
To prove this, we shall consider the following scenario: We
are trying to determine an unknown
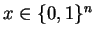 .
We have an oracle
.
We have an oracle
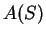 which is supposed to tell us
which is supposed to tell us 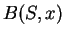 .
The oracle may lie,
but must tell the truth more than half the time. Theorem 34
says we can efficiently enumerate a not-too-large set which
probably includes
.
The oracle may lie,
but must tell the truth more than half the time. Theorem 34
says we can efficiently enumerate a not-too-large set which
probably includes 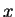 .
.
Theorem 34
Suppose that
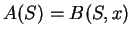
for at least
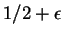
of all
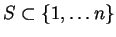
.
We can enumerate
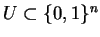
in time polynomial in
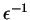
such that
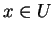
with
probability close to 1.
To deduce Theorem 33 from Theorem 34, suppose we had
an efficient algorithm for guessing 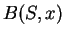 .
We obtain
.
We obtain 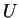 ,
which
cannot be too large given the time bound.
If we are given the value of
,
which
cannot be too large given the time bound.
If we are given the value of 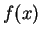 ,
we can evaluate
,
we can evaluate 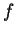 for all
for all 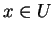 to
identify the correct
to
identify the correct 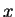 with high probability, which would mean
with high probability, which would mean
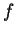 is not a one-way function.
is not a one-way function.
The construction of 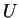 proceeds in stages. At stage
proceeds in stages. At stage 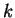 (
(
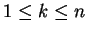 ),
we enumerate
),
we enumerate
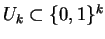 which includes (with probability
close to 1) the first
which includes (with probability
close to 1) the first 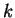 digits of
digits of 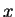 .
.
We will consider 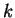 fixed for the rest of this section.
Define
fixed for the rest of this section.
Define
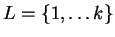 and
and
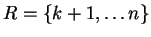 .
If
.
If 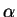 and
and 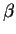 are true or false,
are true or false,
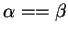 is defined to be 1 if
is defined to be 1 if 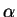 and
and 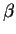 are both
true or both false, 0 otherwise. If
are both
true or both false, 0 otherwise. If 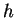 is defined for all
is defined for all
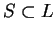 ,
we will use
,
we will use
![$\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
S\end{array}h(S)$](img619.gif) to represent the average value of
to represent the average value of 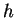 ,
in other words,
,
in other words,
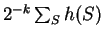 ,
with similar definitions for
other collections of
,
with similar definitions for
other collections of 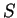 .
The
hypothesis of Theorem 34 can be written as
.
The
hypothesis of Theorem 34 can be written as
Let
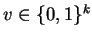 .
If there is a
.
If there is a
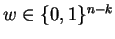 with
with
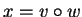 [i.e.,
[i.e., 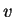 is the first
is the first 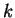 bits of
bits of 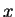 ], then
], then
Recall that 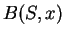 is true if and only if the sum of the bits of
is true if and only if the sum of the bits of 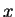 corresponding to
corresponding to 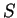 is even. This implies
is even. This implies
Thus, if
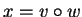 ,
then
,
then
![\begin{displaymath}
\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
D\subset R\end{array}\Bigl(\vert T(v,D)-1/2\vert\Bigr)\ge\epsilon
\end{displaymath}](img629.gif) |
(5) |
To test whether a given 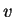 satisfies (5) requires looking at all
possible
satisfies (5) requires looking at all
possible 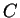 and
and 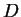 ,
which would take too much time. However, as in
section 7.3, we can take not-too-large random samples from all
possible
,
which would take too much time. However, as in
section 7.3, we can take not-too-large random samples from all
possible 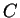 and
and 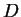 ,
with a high probability of correctly deciding
whether
,
with a high probability of correctly deciding
whether 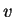 satisfies (5). Let
satisfies (5). Let 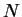 be the number of different
be the number of different
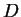 used in the sampling.
used in the sampling.
At stage 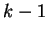 ,
we have obtained
,
we have obtained 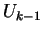 which includes
the first
which includes
the first 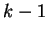 bits of
bits of 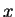 with high probability. To create
with high probability. To create
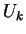 ,
we take each member of
,
we take each member of 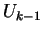 ,
add 0 and 1 to it, and identify using sampling which of the resulting
,
add 0 and 1 to it, and identify using sampling which of the resulting
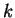 -bit strings satisfy (5).
-bit strings satisfy (5).
This process would take too much time if the number of strings doubled
at each step. To complete the proof, we use
Lemma 35 to show that, for every 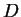 ,
the number of
,
the number of
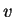 with
with
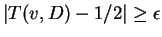 is not too large, specifically
there are at most
is not too large, specifically
there are at most
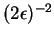 such
such  .
In order to to be included in
.
In order to to be included in  ,
,
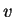 must satisfy
must satisfy
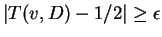 for at least one of the sets
for at least one of the sets 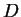 used in the sample,
which gives a bound of
used in the sample,
which gives a bound of
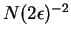 on
on 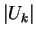 .
.
Lemma 35
For any
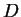
,
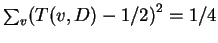
,
where
the sum is over all
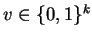
.
Proof: 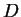 is a constant and may be ignored. We will argue by
induction on
is a constant and may be ignored. We will argue by
induction on 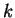 .
Define
.
Define
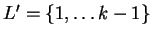 .
The function
.
The function 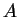 may be represented by
may be represented by 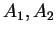 with
with
We divide
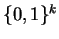 according to whether
according to whether 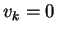 or 1 to obtain
or 1 to obtain
Footnotes
- ... result17
- O. Goldreich and L. Levin, ``A Hard-Core
Predicate for Every One-Way Function,''
Symposium on Theory of Computation (1989)



Next: A recent pseudo-random number
Up: Further results on pseudo-random
Previous: Hard-Core Predicates and Pseudo-Random
Translated from LaTeX by Scott Sutherland
1998-03-15
![$\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
S\end{array}h(S)$](img619.gif) to represent the average value of
to represent the average value of ![\begin{displaymath}\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
S\subset\{1,\ldots n\}\end{array}\left(A(S)==B(S,x)\right)\ge1/2+\epsilon\end{displaymath}](img621.gif)
![\begin{displaymath}1/2+\epsilon\le\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
D\subset...
...L\end{array}\Bigl(
A(C\cup D)==B(C\cup D,v\circ w)\Bigr)\right)\end{displaymath}](img626.gif)
![\begin{displaymath}{\rm Define\quad }T(v,D)=\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
C \subset L\end{array}\Bigl(A(C\cup D)==B(C,v)\Bigr)\end{displaymath}](img627.gif)
![\begin{displaymath}\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
C\end{array}\Bigl(A(C\c...
...1-T(v,D)\quad{\rm if\ }B(D,w){\rm\ is\ false}\end{array}\right.\end{displaymath}](img628.gif)
![\begin{displaymath}
\begin{array}[t]{c}{\rm Avg}\\ [-2pt]
D\subset R\end{array}\Bigl(\vert T(v,D)-1/2\vert\Bigr)\ge\epsilon
\end{displaymath}](img629.gif)
![\begin{eqnarraystar}{\rm Define\quad}T_i(v,D)&=&\begin{array}[t]{c}{\rm Avg}\\ [...
...c12\Bigl(T_1(v,D)+(1-T_2(v,D)\Bigr){\rm\quad if\quad}v_k=1\\
\end{eqnarraystar}](img642.gif)
![\begin{eqnarraystar}\sum_v\bigl(T(v,D)-1/2\bigr)^2&=&\sum_{v_k=0}\left(\frac12T_...
...2\left[\frac14+\frac14\right]
\quad\vrule height 8pt width 4pt\end{eqnarraystar}](img645.gif)