 |
From an early age, we that learn lines and curves are one-dimensional, planes and surfaces are two-dimensional, solids such as a cube are three dimensional, and so on. More formally, we say a set is n-dimensional if we need n independent variables to describe a neighborhood of any point. This notion of dimension is called the topological dimension of a set.4.10 The dimension of the union of finitely many sets is the largest dimension of any one of them, so if we ``grow hair'' on a plane, the result is still a two-dimensional set. We should note here that if we take the union of an infinite collection of sets, the dimension can grow. For example, a line, which is one-dimensional, is the union of an infinite number of points, each of which is a zero-dimensional object.
There can occaisionally be a little confusion about the dimension of an
object: sometimes people call a sphere a three-dimensional object,
because it can only exist in space, not in the plane. However, a sphere
is two-dimensional: any little piece of it looks like a piece of the
plane
![]() 2, and in such a small piece, you only need two coordinates to
describe the location of a point.4.11
2, and in such a small piece, you only need two coordinates to
describe the location of a point.4.11
But, what about the fractals we have been considering? For example, what
is the dimension of the Koch snowflake? It has topological dimension one,
but it is by no means a curve-- the length of the ``curve'' between any
two points on it is infinite. No small piece of it is line-like, but
neither is it like a piece of the plane or any other
![]() n. In some
sense, we could say that it is too big to be thought of as a
one-dimensional object, but too thin to be a two-dimensional object.
Maybe its dimension should be a number between one and two.
In order to make this kind of thinking more precise, let's look at the
dimension of familiar objects another way.
n. In some
sense, we could say that it is too big to be thought of as a
one-dimensional object, but too thin to be a two-dimensional object.
Maybe its dimension should be a number between one and two.
In order to make this kind of thinking more precise, let's look at the
dimension of familiar objects another way.
What is the relationship between an object's length (or area or volume) and its diameter? The answer to this question leads to another way to think about dimension. Let us consider a few examples.
If we try to cover the unit square with little squares of side length
![]() , how many will we need? Obviously, the answer is
1/
, how many will we need? Obviously, the answer is
1/![]() . How about to cover a segment of length 1? Here we need
only
1/
. How about to cover a segment of length 1? Here we need
only
1/![]() little squares. If we think of the square and segment
as sitting in space and try to cover them with little cubes
little squares. If we think of the square and segment
as sitting in space and try to cover them with little cubes ![]() on
a side, we get the same answer. And if we use the little cubes to cover a
1 x 1 x 1 cube, how many will we need? Exactly
1/
on
a side, we get the same answer. And if we use the little cubes to cover a
1 x 1 x 1 cube, how many will we need? Exactly
1/![]() .
Note that the exponent here is the same as the dimension of the thing we
are trying to cover. This is no coincidence.
.
Note that the exponent here is the same as the dimension of the thing we
are trying to cover. This is no coincidence.
We define the box-counting dimension (or just ``box dimension'')
of a set
![]() contained in
contained in
![]() n as follows:
For any
n as follows:
For any
![]() > 0, let
N
> 0, let
N![]() (
(![]() ) be the minimum number of
n-dimensional cubes of side-length
) be the minimum number of
n-dimensional cubes of side-length ![]() needed to cover
needed to cover
![]() . If there is a number d so that
. If there is a number d so that
Note that the box-counting dimension is d if and only if there is some positive constant k so that
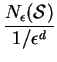 = k.
= k.
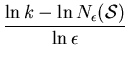 = -
= - 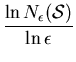 .
.
We should remark that there are some sets
![]() for which
dim
for which
dim![]()
![]()
![]()
![]() cannot be defined because there is no d for
which the limit converges.4.12
We will not encounter such examples here, however. Since the
box-counting dimension is so often used to calculate the dimensions of
fractal sets, it is sometimes referred to as ``fractal dimension''.
We prefer the term box dimension, however, because sometimes the term
``fractal dimension'' might refer to box dimension, Hausdorff
dimension, or even other measures of dimension such as the information
dimension or capacity dimension.
cannot be defined because there is no d for
which the limit converges.4.12
We will not encounter such examples here, however. Since the
box-counting dimension is so often used to calculate the dimensions of
fractal sets, it is sometimes referred to as ``fractal dimension''.
We prefer the term box dimension, however, because sometimes the term
``fractal dimension'' might refer to box dimension, Hausdorff
dimension, or even other measures of dimension such as the information
dimension or capacity dimension.
When computing box dimension, several simplifications can be made.
Sometimes box counting dimension is referred to as ``similarity dimension'' in the context of self-similar sets. If a set is self-similar, there is an expansion factor r by which one can blow up a small copy to get the whole set. If there are exactly N such small copies that make up the entire set, the box dimension is easily seen to be lnN/ln r.
Not surprisingly, the box dimensions of ordinary Euclidean objects
such as points, curves, surfaces, and solids coincide with their
topological dimensions of 0, 1, 2, and 3-- this is, of
course, what we would want to happen, and follows from
the discussion at the beginning of §5.1. But what
about other, more complicated sets? Let's try a few simple examples
for some subsets of the unit interval [0, 1]. In these cases, our
![]() -cubes can be closed intervals of length
-cubes can be closed intervals of length ![]() .
.
Consider the set of points
![]() =
= ![]() 0,
0,![]() ,
,![]() ,
,![]() ,
,![]() ,...
,...![]() . For any n
. For any n![]() 0, we can cover
0, we can cover
![]() with n intervals of length 1/2n: we need one for the elements
between 0 and
with n intervals of length 1/2n: we need one for the elements
between 0 and
![]() , and another interval for each of the
remaining n - 1 elements of
, and another interval for each of the
remaining n - 1 elements of
![]() . This means that
dim
. This means that
dim![]()
![]()
![]()
![]() =
= ![]() n/2n = 0.
The box dimension and the topological dimension of
n/2n = 0.
The box dimension and the topological dimension of
![]() are the
same.
are the
same.
Let
![]() be the set of rational numbers in the interval
[0, 1], that is,
be the set of rational numbers in the interval
[0, 1], that is,
Recall that any real number x can be represented as a (possibly
infinitely long) decimal. For example, 1/4 = .25,
1/11 = .0101![]() ..., and
..., and
![]() = 3.14159265....
The decimal expansion is not quite unique-- for example, 1/2 can be
written as either
.4999999
= 3.14159265....
The decimal expansion is not quite unique-- for example, 1/2 can be
written as either
.4999999![]() ... or
.5000000
... or
.5000000![]() .... This is the only possible point of
confusion, however: any real number x ending in all zeros has
another representation ending in all nines.
.... This is the only possible point of
confusion, however: any real number x ending in all zeros has
another representation ending in all nines.
Let us determine the box-counting dimension of the set
So, what is
dim![]()
![]()
![]()
![]() ? Let's construct a sequence of
covers of
? Let's construct a sequence of
covers of
![]() whose diameter tends to zero, and count the number
of pieces we need. Note that while
whose diameter tends to zero, and count the number
of pieces we need. Note that while
![]() contains the points4.13
.4 and .6, it does not contain the open interval (.4,.6), so we
can cover it by two intervals of length .4, namely [0,.4] and
[.6, 1]. This means
N.4 = 2.
contains the points4.13
.4 and .6, it does not contain the open interval (.4,.6), so we
can cover it by two intervals of length .4, namely [0,.4] and
[.6, 1]. This means
N.4 = 2.
At the next finer level, we can see that
![]() can be covered with
the intervals
can be covered with
the intervals
| [0,.04], | [.06,.10], | [.10,.14], | [.16,.20], | [.20,.24], | [.26,.30], | [.30,.34], | [.36,.40], |
| [.60,.64], | [.66,.70], | [.70,.74], | [.76,.80], | [.80,.84], | [.86,.90], | [.90,.94], | [.96, 1] |
For
![]() = .004, we will need 8 times as many intervals to
cover
= .004, we will need 8 times as many intervals to
cover
![]() . This pattern continues: each time we shrink
. This pattern continues: each time we shrink
![]() by another factor of 10, we need 8 times as many intervals.
by another factor of 10, we need 8 times as many intervals.
This means that
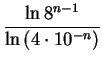 = -
= - 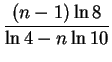 =
=
The box-counting dimension of
![]() is not an integer. Note that
the topological dimension of
is not an integer. Note that
the topological dimension of
![]() is zero.
is zero.