Interpolation vs. Fitting

In what we have been doing so far in this chapter, we have been assuming that there is some sort of error in the data, and that the model we want to fit to our data has some ``wiggle room''. Since our data points are assumed to be approximate, we don't want our resulting curve to pass exactly through them, merely to get as close as possible on average.

This is in sharp contrast to interpolation, in which case the data points are assumed to be known exactly (or at least to very good precision), and a curve of some type is chosen that passes through each of the data points (instead of just as near as possible, in the least squares case.)

Of course, there are serious restrictions to doing this. Since a line is determined by two points, if we have more points, we must either use a higher degree polynomial, or use several line segments. If we have n data points we wish to interpolate, either we can fit a polynomial of degree n - 1 or find n - 1 line segments which ``connect the dots''. We'll address both of these in this section, as well as a method which is a cross between the two approaches.

Polynomial Interpolation

Given n data points (x₁, y₁),(x₂, y₂),...,(x_n, y_n), there is a unique polynomial of degree n - 1 passing through them. Finding this polynomial is just a matter of solving the n linear equations for the coefficients. For example, suppose we have 4 data points (x₁, y₁), (x₂, y₂), (x₃, y₃), and (x₄, y₄). There is exactly one degree 3 polynomial p(x) = ax³ + bx² + cx + d which passes through all four points. Plugging in our data yields the equations

ax13 + bx12 + cx1 + d	=	y1
ax23 + bx22 + cx2 + d	=	y2
ax33 + bx32 + cx3 + d	=	y3
ax43 + bx42 + cx4 + d	=	y4

These are easily solved for the coefficients a, b, c, and d.

Maple 7^2.3 has a built-in command called PolynomialInterpolation to do this automatically for us, as part of the CurveFitting package. We'll do a brief example.

> 
   data:=[[1,3],[2,4],[4,9],[5,11]]:
  

  with(CurveFitting):
   cubfit:=PolynomialInterpolation(data,x);

> 
  plots[display](
    plot(data,style=point,color=black,symbol=BOX),
    plot(cubfit,x=0..6,thickness=2));

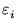
That seems to have worked pretty well. However, polynomials are somewhat stiff: minor variations in the data can have drastic effects on the behavior between the points. To emphasize this, we'll generate 10 points along the line y = 2x + 1, with one more point in the middle that is a bit above the line.

> 
  data2:=[seq([i,2*i+1],i=0..4),[9/2,11],seq([i,2*i+1],i=5..9)];

> 
  plots[display](
    plot(data2,style=point,color=black,symbol=BOX),
    plot(PolynomialInterpolation(data2,x),x=0..9,thickness=2));

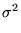
Doesn't look much like a straight line, does it?

Connect the Dots and Splines

As we said at the start of this section, another choice is not to use a single function, but to use several segments which connect the dots. The result would be a piecewise-affine function consisting of several line segments defined on a number of intervals. In the example from the previous section, this function would be

f (x) = $$\cases{ 2x+1 & if $x \le 4 $ \cr 4x-7 & if $4 < x \le \frac{9}{2}$ \cr 11 & if $\frac{9}{2}< x \le 6$ \cr 2x+1 & if $6 < x$}$$

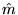
Although writing a maple procedure to figure this out for us would not be hard, such a piecewise affine curve is a version of something called a spline, which we will discuss more soon. This type of connect-the-dots curve is a linear (or degree 1) spline, and Maple can find it using the Spline command out of the CurveFitting^2.4 package.

> 
  lspline:=Spline(data2,x,degree=1):

> 
  plots[display](
    plot(data2,style=point,color=black,symbol=BOX),
    plot(lspline,x=0..9,thickness=2));

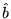
If we leave off the degree=1, Maple gives us a cubic spline instead:

> 
  plots[display](
    plot(data2,style=point,color=black,symbol=BOX),
    plot(Spline(data2,x),x=0..9,thickness=2));

Notice how the cubic spline fits the points about as well as the ``connect-the-dots'' piecewise affine curve, but has no corners. But what is a cubic spline?

To make a spline, instead of connecting each pair of points by a straight segment, we put in a polynomial of degree d. We must ensure that the polynomial passes through the two endpoints of each segment, but this still leaves us an additional d - 1 conditions per polynomial segment. The entire curve can be made smoother by choosing each polynomial segment so that the first d - 1 derivatives at one endpoint agree with the derivatives of the previous segment. Since there is no segment before the first or after the last, this leaves d - 1 more conditions still to specify. For a ``natural spline'', the high order derivatives at the endpoints are set to zero:

p^{(d - 1)}(x₁) = p^{(d - 2)}(x₁) =...= p^{(${\frac{d-1}{2}}$)}(x₁) = 0

and

p^{(d - 1)}(x_n) = p^{(d - 2)}(x_n) =...= p^{(${\frac{d-1}{2}}$)}(x_n) = 0

(if d - 1 is odd, we have one fewer zero derivative at x_n than at x₁). Thus, for a cubic spline, the second derivatives vanish at eachpoint, and the polynomial segments have the same value, slope, and concavity at each interior point.

You might think that using higher degree polynomials in between would give a better appearance, but the same issues that arose in the previous section begin to show up. Note that if we have n data points, fitting a spline of degree n - 1 is exactly the same as the interpolating polynomial of degree n - 1. Cubic splines are the most widely used, because they look quite smooth to the eye, but have enough freedom that they don't have to wiggle too much in order to pass through each data point. Many computer drawing programs have the ability to fit cubic splines through a set of points.

Footnotes

...Maple 7^2.3

earlier versions of Maple have a similar command called interp with slightly different syntax.

...CurveFitting^2.4

versions prior to Maple 7 have a similar command called spline which takes slightly different arguments.