MAT 360 Geometric Structures, Spring 2011.
- Instructor: Olga Plamenevskaya, office 3-107 Math Tower,
e-mail: olga@math.sunysb.edu
- Office hours: Tuesday 12:15-2:15 or by appointment.
- Class meetings: TuTh, 2:20-3:40pm, Physics P112.
- Grader: Caner Koca, office hours: Wed 2-3 in Math 3-118, Wed 3-5 in MLC.
The main goal of the course will be to study the foundations of the Euclidean geometry. We will learn
how to work with geometric images and how to construct careful mathematic arguments. Later in the course, we will
also talk a bit about non-Euclidean geometry.
As this is an upper-level class, familiarity with proofs is expected. Indeed, you will have to write rigorous proofs
in your homework.
- Textbook:
- Kiselev's Geometry, Book I. Planimetry, adapted from Russian by Alexander Givental, Sumizdat, El Cerrito, Calif., 2006.
This is a required text. Unfortunately, it doesn't cover everything we'll discuss in the course; additional notes will be posted here as needed.
Some sample pages of the textbook are available on the publisher's website.
(There's enough for the first week of the course; those who don't have the book yet will find it useful.)
Front Matter (Read the Foreword!)
Pages 1-33
- Exams: there will be two midterm exams and a final exam.
Final Exam: Friday, May 20, 11:15 - 1:45 pm, in Physics P-112 (our usual classroom).
Office hours will be held by appointment. (Wednesday is the best day for me; on Thursday I am
not available. Please email me to set up a meeting if you'd like to come with questions.)
Question topics for the final is here.
Midterm II: Thursday, Apr 28, in class.
The exam will cover the topics we studied since the first midterm,
namely, isometries and similarity.
(You are still reponsible for the previous topics, such as triagles,
circles, parallelograms,etc, but they will not be emphasized.)
Checklist of topics for exam II is here.
Midterm I: Tuesday, Mar 22, in class.
Checklist of topics for exam I is here. (Mostly this is just a list of sections from the textbook.)
The best exam preparation is to go over all past homeworks, and make sure you know how to solve similar
problems. For extra practice, there's plenty of questions in the book.
- Homework: weekly assignments will be posted on
this page. Homework will constitute a significant part of your course grade.
Important: For each homework problem,
please give a proof or detailed explanation as appropriate (unless otherwise stated). Please
write up your solutions neatly, be sure to put your name on the first page and staple all pages.
Illegible homework will not be graded.
You are welcome to discuss homework with others and to consult books,
but your solutions should be written up in your own words,
and all your collaborators and sources should be listed.
Read Lecture notes on non-Euclidean geometry.
Read Lecture notes on inversions and sections 194-197 of the textbook.
(The latter are about the degree of a point with respect to a circle).
Homework 11, due May 12: pdf UPDATED 05/05, 10:30pm
Week 11 (04/11 – 04/15)
Read Lecture notes on similarity, along with sections 143-154, 156-162, 181-183 in the
book.
Homework 10, due April 28: pdf
Week 10 (04/4 – 04/8)
Finish reading lecture notes on isometries. Read sections 143-160 in the textbook.
Homework 9, due April 14:
From the textbook: 332, 336, 338a, 214a (hint for 214: use lemma in section 159),
and one additional question :
We know that isometries of the plane come in four types
(rotations, translations, reflections, glide reflections).
Determine which of these types can be represented by:
a) Composition of a rotation and a translation;
b) Composition of a rotation and a reflection.
Prove your answer. A complete solution must include examples
showing that particular types (say reflections and translations)
can be represented by a required composition, and a proof that
the remaining types (say rotations and glide reflections) cannot
be represented.
Week 9 (03/28 – 04/1)
Read Lecture notes on isometries (updated 04/06)
(These notes were written by Prof. Oleg Viro
in Spring 2010, with some minor changes and additions by Olga Plamenevskaya, 2011.)
Homework 8, due April 7: pdf
There is no homework due Thursday,
03/31.
Week 7 (03/14 – 03/18)
Read sections 9, 10, 103-114, 122-124, 126, 135-136(1), 138-139.
Homework 7, due Mar 24
(it is recommended that
you practice with circles before the exam)
From the textbook: 237, 245, 265, 275.
Week 6 (03/7 – 03/11)
Read sections 86-97, 98-100.
Homework 6, due Mar 17
From the textbook: 179, 180, 190, 191, 192, 197, 210.
Week 5 (02/28 – 03/4)
Read sections 70-82, 84, 85.
Homework 5, due Mar 10
From the textbook: 143, 150, 154, 163, 165, 167.
Week 4 (02/21 – 02/25)
Read sections 61-69.
Homework 4, due Mar 3
From the textbook: 63, 109, 122b, 124, 138.
In construction problems (122b, 124, 138), you can refer to sections 62-67 as known, without repeating all steps.
Justify your construction (prove that the thing you've drawn has required properties).
In 63, try to consider all possible cases, and explain why there can't be more answers.
Week 3 (02/14 – 02/18)
Read sections 51-60.
Homework 3, due Feb 24
From the textbook: 86, 96, 101, 102, and the following extra question.
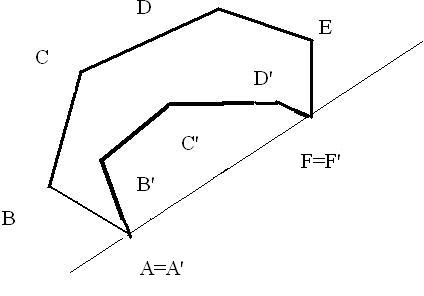
Suppose two convex broken
lines ABCD.. and A'B'C'D'... share the same endpoints and lie on the same side of the line connecting the endpoints,
so that A'B'C'D'... is contained inside ABCD.... Show that the sum of the segments in ABCD... is greater than the sum of the segments
in A'B'C'D'..., ie AB+BC+CD+..>A'B'+B'C'+C'D'+... The broken lines can have different number of segments. See picture.
Start with the case when both broken lines consist of two segments; we considered this in class. What happens if the broken lines are not convex?
For every question, please give detailed proofs/explanations as
appropriate.
Week 2 (02/5 – 02/11)
Read sections 31-33, 39-50.
Homework 2, due Feb 17
From the textbook: 76, 77, 80, 81, 90, 93. Please give detailed proofs/explanations as
appropriate.
Week 1 (01/31 – 02/04)
Read sections 1-8, 13-16, 21-27, 34-38.
(We have discussed most of this in class.) The reading assignments are important because they teach you how to follow the proof
carefully, and how to build your own proofs and to use correct notation.
Homework 1, due Feb 10
Read pages 1-18 of the textbook (contained in the the sample pages).
Find all the instances where properties of isometries of the plane are
implicitly used.
One of the properties is stated explicitly on page 2, lines 2-5:
(i) One can superimpose a plane on itself or any other plane in a way that
takes one given point to any other given point...
Other properties were given in the first lecture:
(ii) One can superimpose a plane on itself or any other
plane in a way that takes one given ray to any other given
ray.
(iii) A plane can be superimposed on itself keeping all the points
of a given straight line fixed. This "flip" can be done in a unique way.
In other words,
(ii) There exists an isometry which maps a plane onto itself or
any other plane in a way that takes one given ray to any other given
ray.
(iii) There exists a unique non-identity isometry of a plane onto
itself keeping all the points of a given straight line fixed.
Your task is to list all the places in the first 18 pages of the
textbook where these properties are used implicitly, ie
without explicit mentioning. Present your solution as a table
with rows:
page number, line number, the property, how the property is used.
(Example: p. 27, line 2, property (iii) is used to "fold" the diagram along the line BD.)
Please also do the following questions from the textbook: 40, 61, 67, 69.
Students with Disabilities: If you have a physical,
psychological, medical, or learning disability that may impact on your
ability to carry out assigned course work, you are strongly urged to
contact the staff in the Disabled Student Services (DSS) office: Room
133 in the Humanities Building; 632-6748v/TDD. The DSS office will
review your concerns and determine, with you, what accommodations are
necessary and appropriate. A written DSS recommendation should be
brought to your lecturer who will make a decision on what special
arrangements will be made. All information and documentation of
disability is confidential. Arrangements should be made early in the
semester so that your needs can be accommodated.
