• Home
  • Introduction
  • Posters
  • Problems
  • Biographies
  • Cool Links
  • The Design Team

    • Analysis

    Analysis is about doing things properly. It is about rigorous proof. There is no hand waving in analysis. Analysis comes in many different flavors.

    Real Analysis

    The "real" in Real Analysis comes from the real numbers. A real number is any number on the number line. It could be a fraction (which we term a rational number), an integer, or even what is called an irrational number. An irrational number is one that cannot be represented as a fraction.

    Try to classify each of the following real numbers. Are they integers, rational, or irrational? Can something be both an integer and rational? Can it be rational and irrational?

    • 2
    • ½
    • p
    • p divided by four
    • the square root of two
    • the square root of eight
    • the square root of eight divided by the square root of two
    By the way, these are important matters. In ancient times, people were allegedly killed by the Pythagoreans for claiming the square root of two was irrational. The Pythagoreans were followers of Pythagoras; you can read more about him at the History of Math site.

    One way to end arguments over things, is by rigorous proof. If you can make an argument rigorous, well, that pretty much ends the argument.

    Can you present a rigorous argument that the square root of two is irrational? Go on, try. Here are some hints.

    Here's another problem. This one is a bit easier. Can you prove that any number which can be written as a decimal that either stops (like 0.234567) or recurrs (like 0.333...) is a rational number? Remember, in analysis it is not enough to sort of, maybe, understand how to do it. You need to be able to write down a proper proof.

    At the heart of Real Analysis is the notion of the limit. To understand this, we need to understand functions.

    A function is like a machine: you feed one number in, and get another out. The important rule is that for each input there is one and only one output. Let's look at some notation:

    f(x)=3x+4
    • f is the name of the function (think of f as standing for Fred).
    • x is a placeholder. It symbolizes the function's input.
    Suppose I want to know what happens when I feed 2 into this machine (we write this as f(2) -- and say, "The f of 2." Notice how 2 replaces x. That's what I mean by x being a placeholder for the input.) Well, we feed 2 into the machine. Chug-a-chug it goes. The instructions on the left of the = sign tell us what the machine does to the input. We have to replace the placeholder, x, with the actual input, 2 -- and we get 3(2) +4, or 10. Writing this out gives,
    f(2)=3(2)+4=10

    Anyway, that's all a function is: a rule for attaching one number to another (in this case the number 10 is attached to the number 2, and it is the only number attached to 2.)

    A function can also be depicted graphically. We can draw two axes: one for the function's input and one for the function's output. Traditionaly, we use the horizontal axis for input (and call it the x-axis) and the vertical (or y-)axis for the output.

    f(x)=3x+4 would have the following picture: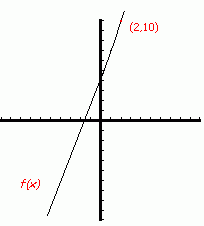


    Several concerns present themselves. Is a given function continuous (that is: can you draw its graph without lifting your pencil?) The function we have been looking at is, but that need not be the general case. Is a given function smooth -- mathematicians use the word differentiable, (which means: does the function have a well-defined slope at every point? The slope of an arbitrary function at any given point, if it exists, is the slope of a tangent line to the function at that point. The slope of a line is "vertical change" divided by "horizontal change".) Again, our function certainly is, but what happens in general?

    These concerns are the beginnings of calculus. Analysis grew out of a need to formalize, to make rigorous, the calculus.

    Notice, that most of these questions are local questions. To know if a function is smooth at the input value of 2, we only need to know what happens near that value.

    The notion of limit makes this precise. By the limit of a function at a specific input value, we mean, "what output value does the function tend to produce as the input values get closer and closer to the specified input value."

    In our given example, the limit of f as the input value gets close to 2 is 10.

    Notice how the definition I have given uses words like "tend to" and "closer". What do these words mean? This was the problem the calculus faced for many years. It was the move to make these notions rigorous which led to modern day Analysis.

    So here's a challenge. The definiton of the limit is one of the most important inventions in all of mathematics. Try to work out what it is. Make your definition as precise as possible. Don't use words like "near" or "close". After you feel you have it, check the official definiton of the limit which mathematicians use.

    You may also want to check out how the notion of limit works for sequences.

    There are many other areas of analysis. Here is a brief tour:

    Complex Analysis

    Some simple equations do not have solutions in the real numbers. Can you think of one? They are typified by things that look like this.

    There is no theoretical reason why you can't posit the existence of solutions to this kind of equation. Complex numbers are the result of enlarging the real numbers so that all polynomial equations have solutions.

    Complex analysis is what happens when you do analysis on these numbers. You can generalize notions of continuity and smoothness to functions whose input variable is complex.

    Read more about complex analysis in the Mathematical Atlas.

    Functional Analysis

    Time to get funky. What if the variables you are considering are themselves functions? What is a function of a function? What does a space whose "points" are functions look like?

    Read more about functional analysis in the Mathematical Atlas.

    There are many other types of analysis (Fourier analysis, harmonic analysis, psychoanalysis -- just kidding!) which you can investigate.

    Read more about analysis in the Mathematical Atlas.