Poster Project: Golden Mean, Continued Fractions and the Fibonacci Sequence

Home

Remember that the Fibonacci sequence is

1, 1, 2, 3, 5, 8, 13, 21, ...

and the rule to generate the next term is to add the two previous terms.

Let's look at the sequence of continued fractions generated by

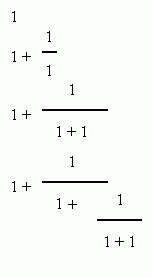The first term is 1. The second term is 1+1/1 or 2. The third term is is 1 + 1/(1+1) or 1+1/2, which is 3/2. The fourth term is 1 + 1/[1 + 1/(1 + 1/1)], which is 1 + 1/[3/2], or 1 + 2/3, which is 5/3. Let's try that sequence down:

1/1, 2/1, 3/2, 5/3, ...

Can you see it's connection to the Fibonacci sequence now?

The sequence generated by this particular continued fraction generates the ratios of succesive terms of the Fibonacci sequence.