4. The disk-sphere-cylinder integrator

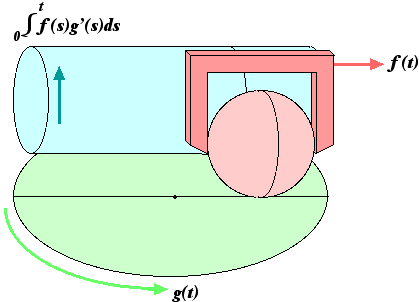
The center of the disk is fixed. The sphere rolls on the disk. Its point of tangency moves back and forth according to the function f(t), with 0 corresponding to the center of the disk. The cylinder has a fixed axis and is driven rotationally by the sphere. Cylinder and sphere have the same radius. The cylinder does not touch the disk.

Between t and t+dt, the disk rotates g'(t) dt radians. Since the sphere is tangent at radius f(t), points on its instantaneous circle of tangency travel f(t)g'(t)dt around an axis parallel to the cylinder, and points on the surface of the cylinder travel the same distance in the opposite direction.

• Setting up the problem

• Almost orthogonality

• The complete calculation

• The disk-sphere-cylinder integrator

Comments:webmaster@ams.org © Copyright 2001, American Mathematical Society