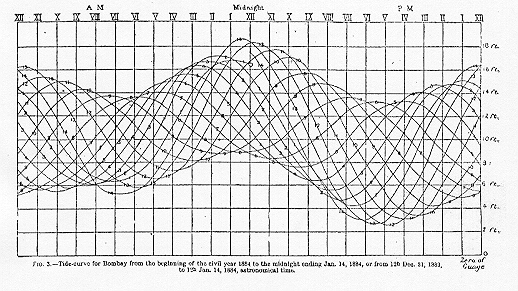
| From George H. Darwin's article "Tides," Encyclopaedia Britannica, IX Ed.,Chicago, 1890. Note that in this graph, time increases to the left. Larger image. |
 Fourier Analysis of Ocean Tides I
Fourier Analysis of Ocean Tides I

| From George H. Darwin's article "Tides," Encyclopaedia Britannica, IX Ed.,Chicago, 1890. Note that in this graph, time increases to the left. Larger image. |
Tides. This figure shows the tidal record for two weeks (January 1-14, 1884) at Bombay. The tide was recorded on a cylindrical sheet that turned once every 24 hours. Each daily curve is labelled with its date. Some obvious features:
| The yearly travel of the Earth around the sun, the monthly travel of the Moon around the Earth, and the daily rotation of the Earth on its axis are the three main rythms that govern the tides. (It is impossible to draw the Sun-Earth-Moon system to scale. To scale, the Sun is a basketball in the center of a football field, the Earth is the eraser on a pencil held on the sidelines, and the Moon is the tip of a straightened-out paper clip stuck in the eraser.) |
In fact the "tidal force" depends on the gradient of the gravitational field. Because (in the case of the lunar tide) what creates the bulge in the Earth's oceans on the side facing the Moon is the fact that the surface of the Earth is closer to the Moon than the center, and is therefore attracted more strongly. This also explains the bulge on the opposite side: there the center is closer than the surface. In general a variable gravitational field will stretch bodies along its gradient; our ocean tides are a special case of this effect.
Why the gradient?
The gravitational force exerted by a body of mass m on a piece
of matter
at a distance L centimeters gives it an acceleration
Gm/L2 cm/sec2,
where G= 6.67x10-8dyne-cm2/g2 is Newton's gravitational constant.
Suppose another piece of matter is k centimeters
farther in the same direction.
Then it undergoes a smaller acceleration: Gm/(L+k)2 cm/sec2.
The difference between these two accelerations can be ascribed to
a ``tidal force"
pulling the two pieces apart. The estimation of this difference is a classic
example of the linear approximation f(x+k) - f(x) ~ k f'(x).
It yields
-2 G m k
--------- cm/sec2.
L3
|
|
|
© Copyright 2001, American Mathematical Society |