
The Differential Geometry of the Sphericon
5. Curvature on the Sphericon: the cone-points
The cone-points on the Sphericon are of a special type, because
they are on the ends of the zip-locus. The Sphericon geographers
can still analyze them using Gauss' Theorem.

In this figure they have drawn a right triangle around one of the cone-points.
One side of the triangle is drawn in blue
using parts of radii. Since radii are perpendicular to the zip-locus, the two pieces fit together without forming a corner in the surface and
form a geodesic edge.
One side of the triangle is drawn in
red using segments perpendicular to the
green line along which the initial gluing is done, so they also fit together
to give another geodesic edge.
- The third side is perpendicular to the red side.
What are the other angles in this triangle? Here a little plane geometry
leads to the answer. The black-blue angle
is 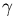 +
+  -
-  ; the red-blue angle is
; the red-blue angle is 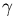 +
+  /2.
/2.
So the sum of the angles in the triangle is 2 -
- +2
+2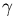 .
.
Gauss'Theorem tells us that the total curvature enclosed in the
triangle is  -
- +2
+2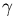 . We can see that the
. We can see that the 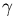 curvature
is coming from the zip-locus. As we take smaller and smaller
such triangles about the cone point, the
curvature
is coming from the zip-locus. As we take smaller and smaller
such triangles about the cone point, the 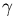 contribution
will go to zero, leaving us with a point-concentration of
curvature at the cone-point equal to
contribution
will go to zero, leaving us with a point-concentration of
curvature at the cone-point equal to  -
- .
.
On to Sphericon page 6.
Back to Sphericon page 4.
© copyright 1999, American Mathematical Society.

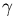 +
+  -
-  ; the red-blue angle is
; the red-blue angle is 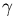 +
+  /2.
/2.
 -
- +2
+2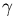 .
.
 -
- +2
+2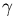 . We can see that the
. We can see that the 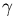 curvature
is coming from the zip-locus. As we take smaller and smaller
such triangles about the cone point, the
curvature
is coming from the zip-locus. As we take smaller and smaller
such triangles about the cone point, the 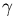 contribution
will go to zero, leaving us with a point-concentration of
curvature at the cone-point equal to
contribution
will go to zero, leaving us with a point-concentration of
curvature at the cone-point equal to  -
- .
.