
Here they have drawn a quadrilateral that is bisected by the zip-locus. (They can do this without actually crossing that locus themselves!). Its red and blue edges are drawn using straight line segments from the cone-points to the zip-circles, so they meet those circles at right angles. In that way, when the zipping is done, each pair of edges fits together without forming a corner as seen in the surface. Since they are both straight line segments before the zipping, they will form a single geodesic edge. The resulting figure has four geodesic edges: one red, one blue and two black.
What are its angles?
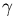 = L/R, in radian measure.
= L/R, in radian measure.
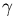 +
+  )/2. The sum of the interior angles is therefore
2(
)/2. The sum of the interior angles is therefore
2(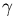 +
+  ).
).  (here n=4), so the total
enclosed curvature is 2
(here n=4), so the total
enclosed curvature is 2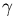 = 2L/R.
= 2L/R.
This calculation does not depend on the height of the quadrilateral away from the zip-locus. The only way to explain the result is to say that the surface curvature is concentrated along the zip-locus in such a way that any curve intersecting the zip-locus in an arc of length L will enclose total curvature 2L/R.
Back to Sphericon page 3.