The rough idea is this.
According to the scaling law whose best known
consequence is Kepler's Third Law, we may as well
assume that the period is
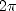 . The orbit obeys the
principle of least action, which means
that locally along the path
the integral of the action A = K.E. - P.E. (the difference
between the kinetic and potental energies) is a minimum.
This suggests that in order to find
a choreography we start with almost any path and try
to deform it into one with the least action compatible
with its topology.
A choreography involving N bodies
is determined by a periodic
smooth curve in the plane.
The components (x(t), y(t))
may therefore be expanded in a Fourier series, the sum
of harmonic terms (cos nt, sin nt). We can't work
practically with an infinite number of terms, so we work
only with truncated Fourier series. This means that we are now
working on a space of finite although possibly very
large dimension. We try to deform the path so as to minimize the action
associated to the choreography, without having the N bodies collide
in the motion associated to any one
of the deformations. To do this we can apply
any one of several possible techniques of numerical
minimization. . The orbit obeys the
principle of least action, which means
that locally along the path
the integral of the action A = K.E. - P.E. (the difference
between the kinetic and potental energies) is a minimum.
This suggests that in order to find
a choreography we start with almost any path and try
to deform it into one with the least action compatible
with its topology.
A choreography involving N bodies
is determined by a periodic
smooth curve in the plane.
The components (x(t), y(t))
may therefore be expanded in a Fourier series, the sum
of harmonic terms (cos nt, sin nt). We can't work
practically with an infinite number of terms, so we work
only with truncated Fourier series. This means that we are now
working on a space of finite although possibly very
large dimension. We try to deform the path so as to minimize the action
associated to the choreography, without having the N bodies collide
in the motion associated to any one
of the deformations. To do this we can apply
any one of several possible techniques of numerical
minimization.
The action associated to a choreography
of N bodies with mass m
on a path q(t) of period T is given by
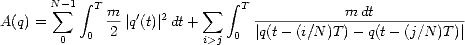 | . |
It is not impractical, using the fast Fourier transform,
to express and calculate this explicitly in terms of the
Fourier coefficients of q, and it is also not much
more difficult to express and calculate
the gradient of A as a function of these coefficients.
So we are reduced to a fairly standard computational
problem: given a function A = A(q1, ... , qn) whose
gradient we can calculate,
how do we find a point where A achieves at least a local minimum?
Theoretically, one could follow down the paths
of steepest descent on the graph of A.
In practice, this leads to disaster.
(Christopher Moore suggests
that that is what he did in the original
discovery of his periodic
orbits, but it is hard to believe that he did so.)
The differential equations x' = -grad(x) one gets will almost
certainly be stiff,
which means that numerical techniques of solving
them are tricky, and to be avoided if possible.
There is a well known technique of minimization,
however, which can be applied successfully - the
conjugate gradient method.
In the following applet, I demonstrate how
action minimization works. We are looking for
a path f(t) = (x(t), y(t)) along which 3 bodies
can run in gravitational equilibrium (i.e. N=3 in the formula for action).
It starts off with
a curve mildly perturbed from the
Lissajous curve (sin t, sin 2t). As it runs, this path
is deformed into the figure-eight choreography orbit
of three bodies first found by Moore.
Here, for demonstration purposes, we use only
Fourier series of 12 terms. (It is important that the number
of bodies divide the number of terms in the Fourier
series. Because the center of mass is fixed at the origin,
the Fourier coefficients whose index is divisible by 3 vanish.) Along the way,
the current action is displayed.
After such a program has been run,
you can check whether or not you have found
a reasonable candidate for a true system by examining the
virtual acceleration along the path. If the orbit
is authentic, then Newton's second Law F = m a is valid,
where the force F is that exerted by the other bodies.
The virtual acceleration of a body at
time t is the function F(t) - m a(t), which will vanish
only for true orbits.
Action minization is not the only way to compute
periodic orbits. Doing it
accurately, especially for complicated orbits, requires
a very large number of terms in the Fourier series (C. Moore
apparently used only 50-60, but Simó has worked
with more than a thousand). This is especially
difficult because in a space of dimension n calculating
the gradient is a task of order n^2 in complexity.
Another possibility is to start with
a point and a velocity, solve the differential equations
arising from Newton's laws, and adjust velocity until
you have come back to the same starting pooint
with the same starting velocity. Simó has in fact
done this, with great success. But even a two-dimensional
`space' is vast when you are contemplating such a task,
and a quick and dirty action minimization is required to give
you some idea of where to probe.
References
In addition to
References:
-
William H. Press,
Brian P. Flannery,
Saul A. Teukolsky, and
William T. Vetterling,
Numerical Recipes - the art of scientific computing,
Cambridge University Press, in any of several
edition.
|
This book is well known for the thoroughness of its
coverage as well as the sloppiness of its code. Chapter 10,
on minimization, is nonetheless one of the best general references
for the conjugate gradient method, particularly for
the crucial one-dimensional
minimization routine called repeatedly by the higher-dimensional one.
Beware: in the edition I have, a sign
is wrong in the formula for a parabolic minimum in one dimension,
in the text and in the printed code as well.
|
-
Jonathan Richard Shewchuk, An introduction
to the conjugate method without the agonizing pain,
http://www.cs.berkeley.edu/~jrs/, 1994.
|
These popular notes, as far as I know
otherwise unpublished, are largely concerned with using the conjugate
gradient method in algorithms of linear algebra.
The discussion of how to use it for non-linear minimization problems
is somewhat skimpy - perhaps even slightly misleading - but the copious pictures
nonetheless make it a valuable source. It serves well to
supplement the somewhat cryptic motivation in Numerical Recipes,
which has few (mediocre) pictures.
|
|

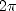 . The orbit obeys the
principle of least action, which means
that locally along the path
the integral of the action
. The orbit obeys the
principle of least action, which means
that locally along the path
the integral of the action