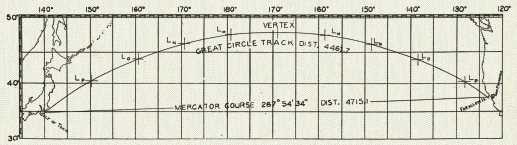
A great circle track plotted on a Mercator chart. From Dutton's "Navigation and Nautical Astronomy", 7th Ed. Reproduced by permission from the U.S. Naval Institute.

Let us go back to the properties of the Mercator projection:
latitudes and longitudes go to an orthogonal grid, and the
projection is conformal. Conformality means that at any point
the vertical and horizontal stretching are the same. If we
use longitude L and height h (measured in the same units as
longitude) as coordinates on the map, then the equator is
not stretched at all: it and its image have length
$360^{\circ}$.
But a circle of latitude at latitude $\lambda$
$360^{\circ} \cos \lambda$
on the sphere, and the same length
as the equator in the Mercator projection. It has been stretched
by a factor
$(1/\cos \lambda) = \sec \lambda$.
For conformality,
the meridians must be stretching by
$\sec \lambda$
as they pass through latitude $\lambda$,
more and more in
higher and higher latitudes. In terms of calculus,
$dh/d\lambda = \sec \lambda$.
In order to apply calculus to the problem it is most
convenient to work entirely in radian measure, and convert
to degrees at the end. In radians, we have two points
on the sphere, one at latitude
$3^{\circ}42'= 0.658$
the other at latitude
$34^{\circ}50'= 0.608$
and
separated by
$97^{\circ}03'= 1.694$
in longitude.
The height h on the map corresponding to latitude $\lambda$
$\int_0^{\lambda}\sec x ~dx$.
This integral, the bane of
generations of Freshmen, has a useful application! As they learned,
$\int \sec x~ dx =
\ln |\sec x + \tan x| + C.$
So latitude
$\lambda=.658$
corresponds to height $h=.711$, and
$\lambda=.608$
to $h=.649$.
The function
$h= \ln|\sec x + \tan x|$
is invertible; in fact
the formula can be explicitly inverted. First write
MATH: $\sec x + \tan x$
as
$\tan(\pi/4+x/2)$
and note that the function is
positive on the sphere so the absolute value signs can
be discarded. Then solve for $x$ to get
$x = 2 \arctan e^h - \pi/2$.
Call this function $G(h)$.
On the Mercator map, the straight line
from $A$
$(h=.711, L=0)$
to $B$
$(h=.649, L=1.694)$
is $t\rightarrow (.711-.062t, 1.694t), 0\leq t\leq 1$.
The rhumb line on the sphere is therefore
The metric on the sphere is $ds^2= d\lambda^2 + \cos^2\lambda dL^2$ so the length of the rhumb line is
Since $G$ is the inverse of a function with derivative
$\sec \lambda$,
the
derivative of G is
$$G'(h) = 1/\sec(G(h)) = \cos(G(h))$$
so the first term inside the radical is
$.062^2 \cos^2(G(.711-.062t))$
while the second term
is
$1.694^2 \cos^2(G(.711-.062t))$.
The radical thus
simplifies to
The length integral is now
The moral of the story is that the great circle track from the Farallones to Tokyo is 234 nautical miles shorter than the straight line between them on the Mercator map, as we have computed them.

Dutton's rhumb line calculation is different from mine, and takes into account the earth's eccentricity e = .082483399. The tables used in Mercator sailing, and the java applets available on the web, take this factor into account: instead of $h = \ln[\tan(\pi/4+x/2)]$ they use
Converted using MathJax December 16 2019.
5. Calculation of rhumb line distance