
II. The Jordan normal form and the structure of abelian groups
Two ![]() matrices A and B are similar if there is an
invertible
matrices A and B are similar if there is an
invertible ![]() matrix S such that
B=S-1AS. This means
that A and B are ``doing the same thing'' but seen with respect
to two different sets of basis vectors.
matrix S such that
B=S-1AS. This means
that A and B are ``doing the same thing'' but seen with respect
to two different sets of basis vectors.
Any ![]() matrix A with complex entries is similar to
a matrix in Jordan normal form. This is a matrix of the
form
matrix A with complex entries is similar to
a matrix in Jordan normal form. This is a matrix of the
form
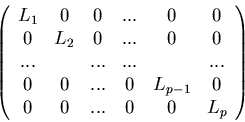

for some complex number ![]() .
.
The metaphier. The structure theorem for finite abelian groups
says that a finite abelian G is isomorphic to a direct sum of
cyclic groups
![]() ,
where ri is a
power of a prime, and that this decomposition is unique up to
ordering. For example, an abelian group of order 12 must be
isomorphic to either
,
where ri is a
power of a prime, and that this decomposition is unique up to
ordering. For example, an abelian group of order 12 must be
isomorphic to either
![]() or
or
![]() .
There are no other
possibilities. This generalizes to
a structure theorem for modules over a principal ideal domain.
.
There are no other
possibilities. This generalizes to
a structure theorem for modules over a principal ideal domain.
![]() and the ring
and the ring
![]() of complex-valued polynomials
are both p.i.d.s; an abelian group is naturally a
of complex-valued polynomials
are both p.i.d.s; an abelian group is naturally a ![]() -module,
with
-module,
with
![]() (n times).
(n times).
The metaphor. Use A to make ![]() into a
into a
![]() -module
by letting
-module
by letting
![]() so
so
![]() ,
etc. The analogue of
,
etc. The analogue of ![]() mod
the multiples of ri (a prime power) is
mod
the multiples of ri (a prime power) is
![]() mod
the multiples of
mod
the multiples of
![]() ,
since in
,
since in
![]() the irreducible
polynomials are linear.
the irreducible
polynomials are linear.
By the structure theorem, ![]() splits up into subspaces
splits up into subspaces
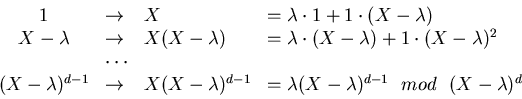
(For more details see a text like Hartley and Hawkes, Rings, Modules and Linear Algebra,Chapman & Hall, London, New York, 1970 or Serge Lang, Algebra, Addison-Wesley 1971.)
5. Metaphors from modern mathematics:
II. The Jordan normal form and the structure of abelian groups