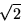The most irrational number
Irrational numbers and the growth of plants
 Tracing the stems of the elements in a pine cone back to the
core shows that they are added one by one, starting at the bottom.
The angle between one stem and the next is always the same. It
is reasonable to suppose that, in
general, the most efficient packing will occur when this angle is
as irrational as possible. This would explain why the "golden mean"
angle, and angles related to it, occur so often in nature.
Tracing the stems of the elements in a pine cone back to the
core shows that they are added one by one, starting at the bottom.
The angle between one stem and the next is always the same. It
is reasonable to suppose that, in
general, the most efficient packing will occur when this angle is
as irrational as possible. This would explain why the "golden mean"
angle, and angles related to it, occur so often in nature.
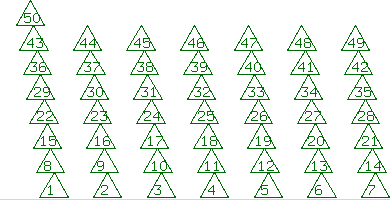
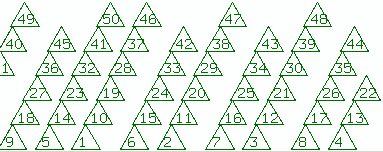
A simplified form of this phenomenon can be illustrated by "packing" triangles
around a cylinder. In these images, the cylinder has been sliced
and rolled out flat. The circumference is set equal to 1. The
x-coordinate of each new triangle is taken to be a constant spacing
d to the right of the one before, with "angles" always reduced modulo 1.
Seed size = .075, spacing = 
Seed size = .075, spacing = 7/31

Seed size = .075, spacing = 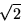
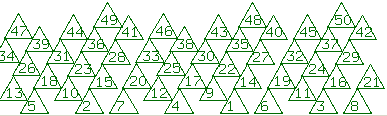
Seed size = .075, spacing = g
Using the "golden mean" spacing g,
as the seed size varies, the different convergents manifest
themselves: different combinations of Fibonacci
numbers appear as the number of left and right-hand "spirals":
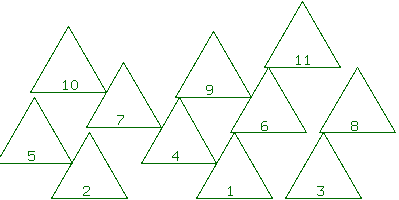
(3,5): Seed size = .2, spacing = g.
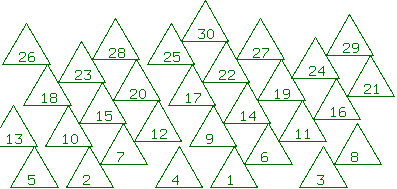
(5,8): Seed size = .125, spacing = g.

(8,13): Seed size = .075, spacing = g.
Food for thought: Experiment with the
computer program that
produced these images. Can convergents always be detected graphically?
Would the effect be different if a different-shaped seed had been
drawn? Can you find a recursive formula for the numerators
and denominators of the convergents for 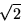 along the lines of the recursive formula for the Fibonacci numbers?
along the lines of the recursive formula for the Fibonacci numbers?
Back to first irrational page.
Back to previous irrational page.
© copyright 1999, American Mathematical Society.
 Tracing the stems of the elements in a pine cone back to the
core shows that they are added one by one, starting at the bottom.
The angle between one stem and the next is always the same. It
is reasonable to suppose that, in
general, the most efficient packing will occur when this angle is
as irrational as possible. This would explain why the "golden mean"
angle, and angles related to it, occur so often in nature.
Tracing the stems of the elements in a pine cone back to the
core shows that they are added one by one, starting at the bottom.
The angle between one stem and the next is always the same. It
is reasonable to suppose that, in
general, the most efficient packing will occur when this angle is
as irrational as possible. This would explain why the "golden mean"
angle, and angles related to it, occur so often in nature.