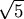 + 1)/2 = 1.618033...
+ 1)/2 = 1.618033...

The most irrational number turns out to be a number already well known in geometry. It is the number
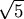 + 1)/2 = 1.618033...
+ 1)/2 = 1.618033...
which is the length of the diagonal in a regular pentagon of side length 1. This number, known as the "golden mean," has played a large role in mathematical aesthetics. It is not clear whether its supreme irrationality has anything to do with its artistic applications.
The golden mean satisfies the equation x2 - x - 1 = 0, so its continued fraction expansion is the simplest of all:
g = 1 + 1
------
1 + 1
------
1 + 1
------
1 + etc.
Its convergents are 1, 2, 3/2, 5/3, 8/5, ... , the ratios of consecutive Fibonacci numbers.
How well are these convergents approximating g? Here are the first few E/M ratios:
convergent E/M c1 = 1/1 1.382 c2 = 2/1 .8541 c3 = 3/2 1.055 c4 = 5/3 .9787 c5 = 8/5 1.008 c6 = 13/8 .9968 c7 = 21/13 1.001 c8 = 34/21 .9995 ...
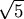 in Hurwitz'
theorem cannot be improved!)
in Hurwitz'
theorem cannot be improved!)
So the golden mean can never have a rational approximation as good
as 22/7 was for 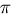 or even as good as
7/5 was for
or even as good as
7/5 was for  .
.
Back to previous irrational page.
Back to first irrational page.
|
© copyright 1999, American Mathematical Society. |