
Calculating high-order derivatives of a function like
![]() can be very messy. A useful theorem reduces the calculation
to combinatorics.
can be very messy. A useful theorem reduces the calculation
to combinatorics.
Wick's theorem
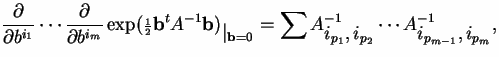
Let us calculate a couple of examples.
To begin, it is useful to write
![]() with
with
![]() (the sums running from 1 to d)
using the series expansion
exp x = 1 + x +x2/2 +x3/3! ... .
The typical term
will be
(the sums running from 1 to d)
using the series expansion
exp x = 1 + x +x2/2 +x3/3! ... .
The typical term
will be
![]() . This term is a homogeneous polynomial
in the bi of degree
2n
. This term is a homogeneous polynomial
in the bi of degree
2n
Differentiating k
times a homogeneous polynomial
of degree 2n
and evaluating at zero will give zero unless
k = 2n.
So the job is to analyze
the result of 2n
differentiations on
![]() .
.
The differentiation carried out most frequently in these calculations is
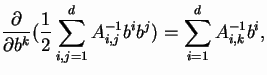
In what follows
![]() will be abbreviated as
will be abbreviated as
![]() .
.
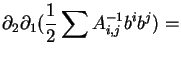
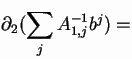 A-11,2,
A-11,2,
Similarly:
|
|
|
© Copyright 2001, American Mathematical Society |