Math and the Musical Offering

7. The transformation  g(t) = f(18-t)  and Canon 1

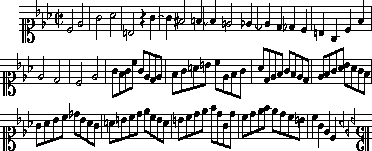
Graphic © 1996, Timothy A. Smith, used by permission.

``Cancrizans'' means ``crab-wise'' but in fact in this canon Voice 2 plays the score of Voice 1 backwards. This is indicated in Bach's cryptic presentation by the backwards signature at the end of the piece. Voice 1 plays the Royal Theme itself (8.5 measures), followed by 9.5 measures of counterpoint.

This score is 18 measures long. For a function g defined on that interval to be the ``backwards'' of f, we need g(0) = f(18), g(1) = f(17), etc. This is achieved by defining

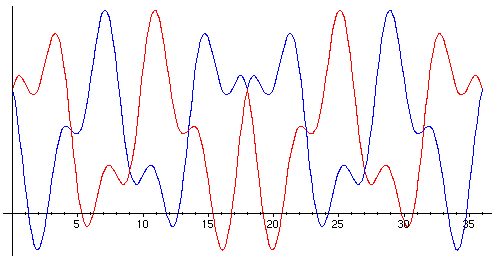
In this plot, as usual, f is the red graph and g is the blue, although in this case the operation is symmetric, and f runs g backwards also.
Usually in performance each player plays his or her score forwards and then backwards (if the instruments are different this is not the same as running through the piece twice). This results in the pattern:

Food for thought: there is one elementary transformation of functions that does not appear in any of Bach's canons. Which is it and why?

• Introduction

• What is a Canon?

• g(t) = f(t-1) and Canon 2

• g(t) = f(t-1) + H and Canon 5

• g(t) = -f(t-0.5) + K and Canon 3

• g(t) = -f((t-0.5)/2) + L and Canon 4

• g(t) = f(18-t) and Canon 1