| Through Mazes |
 |
to Mathematics |
| Through Mazes |
|
to Mathematics |
This page
in Romanian
This page in Polish
This page in Uzbek
This page in Ukranian
This page in Georgian
This page in Swedish
This page in Thai
This page in Kazakh
This page in Hungarian
This page in Finnish
This page in Italian
This page in Turkish.
The best known of these mazes is the Cretan maze.
It can
be drawn as a game.
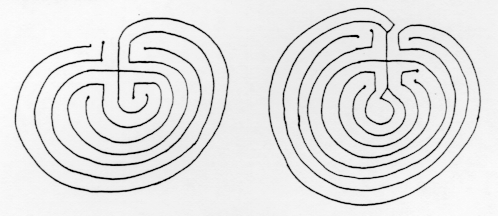
Here is another example. This maze appears in
several medieval hebrew manuscripts.
Although this maze has a
superficial resemblance to the Cretan maze, a close comparison shows
they
are quite different. The Jericho maze has 7 levels, whereas the
Cretan maze
has 8, and the sequence in which the levels are reached differs
from one maze to the other. In both mazes the path goes
directly to level 3 (counting the outside as 0) but in the Cretan maze
it then doubles back through levels 2 and 1, whereas in the Jericho maze
it continues on through levels 4 and 5 before returning to 2 and 1. The
complete level sequences are
Cretan 032147658
Jericho 03452167.
The properties that these two mazes share, and that will serve to define a class of mazes with a simple mathematical description, may be summarized by calling them simple, alternating, transit mazes (s.a.t. mazes).
TRANSIT mazes because the path runs without bifurcation from the outside
of the maze to the center. For example these mazes
are not transit mazes:
in one, the path comes out on the same side it entered; and in
the other there are
points where the maze-runner must choose which way to go.
ALTERNATING because
the plan of the maze is laid out on a certain number of concentric
or parallel levels, and the maze-path changes
direction whenever it changes level.
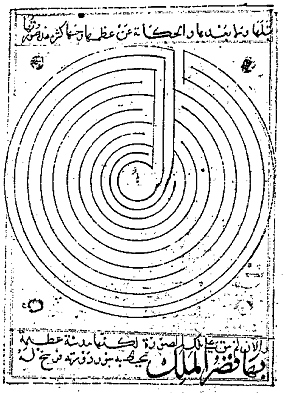
For example this maze,
which represents the plan of Constantinople in a medieval Arabic
geography book has distinct levels but is
not alternating, since it spirals from level 10 to level 1 without
changing direction. Its level sequence 0.3.4.5.6.7.8.9.10.1.2.11
cannot occur, as we shall see, as the
level sequence of an
alternating maze.
SIMPLE because the path makes
essentially a complete circle at each level;
in particular it travels on each level exactly once.
For example, this
alternating transit
maze,
which occurs as a pavement maze in Chartres (shown here)
and in several other cathedrals, and
carved on a pillar in the Cathedral in Lucca,
is not simple: there are four different points at which the path
can change levels. This maze-pattern seems to have occurred as
a christian elaboration and amplification of the cretan design
and its roman descendants; the association with the Theseus myth
persisted. The new design was remarkably persistent itself.
It is seen in medieval manuscripts
dating from the 9th century;
Chartres cathedral was built around the year 1200; and in the
early 16th century the identical pattern is painted on a
florentine
cassone. It is now rendered 3-dimensionally, with
an armored Theseus
battling the Minotaur in the center.
Return to Main Maze Page
Return to Tony's Home Page